Оглавление

• Арифметика целых чисел
  • Основная теорема арифметики
  • НОД и НОК в $\mathbb{Z}$
  • Алгоритм деления в $\mathbb{Z}$

Арифметика целых чисел

---

1.9 в первом томе кострикина

делитель, кратность, отношение делимости, простые числа, основная теорема арифметики, теорема евклида, НОД и НОК, свойства НОД и НОК, взаимно простые числа

---

Основная теорема арифметики

Теорема. Каждое положительное целое число $n>1$ может быть записано в виде произведения простых чисел: $n=p_1{p}_2\dots p_m$. Эта запись единственна с точностью до порядка множителей. Можно сгруппировать одинаковые множители и получить запись вида $n=p_1^{{ϵ}_1}{p}_2^{{ϵ}_2}\dots p_k^{{ϵ}_k}$. Аналогичное (и тоже единственное с точностью до порядка множителей) разложение можно сделать для рациональных чисел.

(Доказательство основной теоремы арифметики будет дано позже. Первая её часть кажется довольно очевидной, однако со второй всё не так просто. Например, рассмотрим вот такое множество $S=4k+1\mid k=0,1,\dots$. Индукцией по $k$ можно доказать существование разложения для чисел из $S$ на квазипростые числа — те, которые нельзя разложить ещё сильнее и они представляются просто как $4k+1$, но я вообще не понял, как это доказывать, и как делать индукционный переход. Но при этом нет единственности такого разложения: например, $441=9\times 49={21}^2$. Так что для просто целых чисел единственность тоже не особо очевидна.)

Теорема Евклида. Множество всех простых чисел бесконечно. Если бы существовало конечное множество $P=p_1,p_2,\dots ,p_n$ простых чисел, то по предыдущей теореме число $c=p_1{p}_2\dots p_n+1$ делилось бы хотя бы на одно из чисел из $P$ (НУО, пусть это будет $p_1$, то есть $c=p_1{c}^{\prime }$). Тогда:

$$\begin{gathered} p_1{c}^{\prime }=p_1{p}_2\dots p_n+1 \\ {p}_1(c^{\prime }-p_2\dots p_n)=1 \end{gathered}$$

Однако последнее равенство невозможно, потому что делителем единицы может быть только $\pm 1$, а $p_1\ne 1$.

---

НОД и НОК в $\mathbb{Z}$

Определения наибольшего общего делителя и наименьшего общего кратного через основную теорему арифметики. Пусть у нас есть целые числа $m$ и $n$, которые раскладываются на простые следующим образом: $n=\pm p_1^{{\alpha }_1}\dots p_k^{{\alpha }_k}$ и $m=\pm p_1^{{\beta }_1}\dots p_k^{{\beta }_k}$ (для каждого из чисел выписываем все простые, которые делят и то, и другое число, пихаем нули в степени просто, если что). Тогда НОК и НОД определяются вот так:

• НОД$(n,m)=p_1^{min({\alpha }_1,{\beta }_1)}\dots p_k^{min({\alpha }_k,{\beta }_k)}$
• НОК$(n,m)=p_1^{max({\alpha }_1,{\beta }_1)}\dots p_k^{max({\alpha }_k,{\beta }_k)}$

Свойства НОД и НОК:

• НОД$(n,m)\mid n$ и НОД$(n,m)\mid m$ (следует просто по смыслу и из определения).

• Если $d\mid n$ и $d\mid m$, то $d\mid \text{НОД}(n,m)$ (потому что, если $d$ делит и $m$, и $n$, то это означает, что в нём вхождений каждого простого числа меньше или равно минимуму вхождений для $m$ и $n$). То есть, если есть какой-то общий делитель двух чисел, то он будет делить и их наибольший общий делитель.

• $n\mid \text{НОК}(n,m)$ и $m\mid \text{НОК}(n,m)$ (просто по определению).

• Если $n\mid d$ и $m\mid d$, то $\text{НОК}(n,m)\mid d$ (ну тут такое же объяснение, как и для аналогичного утверждения для НОД, это всё видно из разложения на простые числа). То есть наименьшее кратное двух чисел делит любое число кратное обоим этим числам.

• Очевидно, если перемножить НОД и НОК двух чисел, то получится просто произведение этих двух чисел (потому что одно берёт минимумы, другое — максимумы, если всё свалить вместе, то можно будет собрать оба числа): $\text{НОД}(n,m)\times \text{НОК}(m,n)=n\times m$. (Ну, формально тут надо ещё указать, что надо, чтобы $n>0$ и $m>0$)

Числа называются взаимно простыми, если их НОД равен 1.

---

Алгоритм деления в $\mathbb{Z}$

Теорема про деление с остатком. Для любых $a,b\in \mathbb{Z},b>0$ найдутся такие $q,r\in \mathbb{Z}$, что:

$$a=bq+r,0\le r<b$$

(А, если позволить $b$ быть и отрицательным, то условие для $r$ будет вот таким: $0\le r<|b|$.)

Доказательство. Рассмотрим вот такое множество $S=a-bs\mid s\in \mathbb{Z},a-bs\ge 0$ (короче, это все неотрицательные числа, которые получаются последовательными вычитанием и прибавлением $b$ к $a$). Очевидно, это множество непустое, по крайней мере можно взять $s=-a^2$ и тогда $a+b{a}^2=a(1+ab)\ge 0$, потому что, если $a<0$, то $ab\le -1$.

Раз множество непустое, то можно выбрать наименьший его элемент (или только инфимум? ну, это детали), который обозначим за $r=a-bq$, который по определению $S$ будет неотрицательным. Пойдём от противного: предположим, что $r\ge b⟹r-b=a-b(q+1)\ge 0$ — это тоже элемент множества $S$ и он меньше $r$, что противоречит с тем, что $r$ — наименьший элементт S.

Альтернативное определение НОД и разложение НОД. Рассмотрим множество линейных комбинаций целых чисел $m$ и $n$ (таких, что они одновременно не равны нулю): $J=nu+mv\mid u,v\in \mathbb{Z}$. Выберем в этом множестве наименьший положительный элемент $d=n{u}_0+m{v}_0$. А теперь разделим $n$ на это вот $d$:

$$\begin{gathered} n=dq+r,0\le r<d \\ r=n-dq=n-(n{u}_0+m{v}_0)q=n(1-u_{0}q)+m(-v_{0}q)\in J \end{gathered}$$

То есть остаток от деления $n$ на $d$ попадает в это множество $J$. НО остаток от деления меньше, чем $d$, так что он может только равняться нулю, потому что иначе было бы противоречие с тем, что $d$ — наименьший положительный элемент $J$. А раз остаток от деления равен нулю, то $d\mid n$. Аналогично $d\mid m$. И при этом ещё, если есть какой-то другой делитель $d^{\prime }\mid n,d^{\prime }\mid m$, то он будет делить и $d$: $d^{\prime }\mid d=n{u}_0+m{v}_0$.

Таким образом, $d$ удовлетворяет всем характеристическим свойствам НОД, так что можно вот так определить НОД как наименьшую неотрицательную линейную комбинацию чисел. В частности, два числа являются взаимно простыми тогда и только тогда, когда $mu+nv=1$ для некоторых $u,v\in \mathbb{Z}$.

Отсюда же следует обоснование для алгоритма Евклида (на самом деле, нет). Чтобы найти НОД двух чисел, надо взять какой-то элемент $J$ и последовательно его уменьшать, вычитая из него другие элементы $J$ (элементы $J$ замкнуты относительно плюса и минуса). Хотя, нет, как-то не очень, мда, там можно гораздо проще доказать, что алгоритм Евклида корректен.

Оглавление

• Перестановки
  • Перестановки
  • Циклическая структура перестановки
  • Знак перестановки
  • Действие Sn на функциях

Перестановки

---

1.8 в первом томе кострикина

перестановки, симметрическая группа, циклическая запись перестановок, порядок перестановки, орбиты, длина орбиты, единственность разложения на циклы, разложение на транспозиции (циклы длины 2), знак (чётность) перестановки, независимость чётности перестановки от разложения, чётность произведения перестановок, формула для определения чётности, перестановка перестановок

действие перестановок на функции, кососимметрические функции (с примером), доказательство независимости чётности перестановки от разложения через кососимметрические функции

---

Перестановки

Перестановкой называется биективное отображение конечного множества $\mathrm{\Omega }=1,2,\dots ,n$ (сами элементы не важны, поэтому просто для удобства обозначим их циферками) самого на себя. Это отображение $\pi :i\to \pi (i)$ можно ещё записать вот в такой форме:

$$\pi =\left(\begin{array}{cccc}1& 2& \dots & n\\ i_1& i_2& \dots & i_n\end{array}\right)$$

Сверху записаны элементы множества $\mathrm{\Omega }$, а снизу записано то, куда каждый из них отображается: $\pi (k)=i_k$. Ну, это такая, дефолтная запись перестановки, с помощью которой в том числе удобно перемножать перестановки:

$$\sigma \tau =\left(\begin{array}{cccc}1& 2& 3& 4\\ 2& 3& 4& 1\end{array}\right)\left(\begin{array}{cccc}1& 2& 3& 4\\ 4& 3& 2& 1\end{array}\right)=\begin{array}{cccc}1& 2& 3& 4\\ \downarrow & \downarrow & \downarrow & \downarrow \\ 4& 3& 2& 1\\ \downarrow & \downarrow & \downarrow & \downarrow \\ 1& 4& 3& 2\end{array}=\left(\begin{array}{cccc}1& 2& 3& 4\\ 1& 4& 3& 2\end{array}\right)$$

Так как множество перестановок $S_n$ обладает свойствами ассоциативности, есть единичный элемент (перестановка, которая каждый элемент отображает сам в себя) и для каждого есть обратная перестановка, то $S_n$ образуют группу, которая называется симметрической группой степени n. $|S_n|=n!$ — ну это как бы да, очевидно.

---

Циклическая структура перестановки

Перестановки можно раскладывать в произведение нескольких более простых перестановок. Получается более удобная и при кольная запись. Например, если перестановка имеет вид $\pi (i)\to (i\mathrm{mod}4)+1$, то её можно записать в виде $\sigma =(1234)$: здесь числа переводятся в те, которые следуют за ними, и предполагается, что эта штука циклически замкнута. Перестановка может состоять и из нескольких непересекающихся циклов: $\tau =(14)(23)$. Так что получается, что ${\sigma }^4=e$ и ${\tau }^2=e$ — если возвести в наименьшее общее кратное длин циклов перестановки, получим единичную перестановку. Очевидно, то вот эти циклические штуки можно записывать с разными ротациями, это сути не меняет.

Возведение перестановки в степень. Так как перестановка — это биективное отображение из конечного множества в конечное, то обязательно найдётся такая степень ${\pi }^k=\pi (\pi \dots \pi (i))$, что ${\pi }^k=e$. Множество конечно, значит, найдутся такие $m$ и $n$, $m>n$, что ${\pi }^m(i)={\pi }^n(i),\mathrm{\forall }i\in \mathrm{\Omega }$, потому что существует конечное число способов отобразить $\mathrm{\Omega }$ само в себя. $\pi ({\pi }^{m-1}(i))=\pi ({\pi }^{n-1}(i))$, и в силу инъективности (на самом деле, тут достаточно только её, сюръективность следует из всего этого) по значению функции можно однозначно определить соответствующий аргумент, так что можно сократить: ${\pi }^{m-1}(i)={\pi }^{n-1}(i)$. И так сокращаем до упора и получаем ${\pi }^{m-n}(i)=e(i)$.

Кстати, это же самое работает и для любой инъективной функции на конечном множестве, и из последнего вывода следовала бы её сюръективность, потому что $\pi ({\pi }^{m-n-1})=e$, то есть любому значению $i\in \mathrm{\Omega }$ соответствует аргумент ${\pi }^{m-n-1}(i)$.

Степень перестановки, кстати, определяется индуктивно вот так:

$${\pi }^s=\{\begin{array}{ll}\pi ({\pi }^{s-1}),& \text{если }s>0,\\ e,& \text{если }s=0,\\ {\pi }^{-1}(({\pi }^{-1}{)}^{-s-1}),& \text{если }s<0.\end{array}$$

(Короче, просто, если степень положительная, то это несколько умножений $\pi$ самого на себя, если отрицательная — то это несколько умножений ${\pi }^{-1}$ самого на себя. Я не знаю, зачем я написал это, просто я сначала чего-то совсем не понял, что имеется в виду в этой формуле.)

Порядком перестановки называется такое наименьшее число $q\in {\mathbb{Z}}_{>0}$, что ${\pi }^q=e$ (ну и, соответственно, получится так, что все различные степени будут содержаться в множестве $e,\pi ,\dots ,{\pi }^{q-1}$).

Эквивалентные точки. Назовём две точки $i,j\in \mathrm{\Omega }$ $\pi$-эквивалентными, если $j={\pi }^s(i)$ для некоторого $s\in \mathbb{Z}$. Это будет отношением эквивалентности, так как, очевидно, любая точка эквивалентна сама себе (${\pi }^0=e$), это отношение симметрично и транзитивно. Так что перестановка разбивает множество $\mathrm{\Omega }$ на несколько классов экивалентности, которые называются $\pi$-орбитами: $\mathrm{\Omega }={\mathrm{\Omega }}_1\cup \cdots \cup {\mathrm{\Omega }}_p$. Количество элементов в классе эквивалентности — это длина орбиты. Если у нас есть элемент орбиты, то все остальные можно найти, последовательно применяя к нему перестановку.

Определение циклов перестановки. Каждой орбите можно сопоставить цикл длины $l_k=|{\mathrm{\Omega }}_k|$, который определяется вот так:

$${\pi }_k:=(\begin{array}{cccc}i& \pi (i)& \dots & {\pi }^{l_k-1}(i)\end{array})$$

То есть получается перестановка, которая применяет ко всем элементам $i\in \mathrm{\Omega }\setminus {\mathrm{\Omega }}_k$ перестановку $\pi$. Так что любая перестановка разбивается на такие независимые циклы: $\pi ={\pi }_1{\pi }_2\dots {\pi }_p$. При этом не имеет значения, в каком порядке они расположены, потому что они друг от друга не зависят. При этом в записи естественно опускать циклы длины 1.

Единственность разложения на циклы.

При этом можно всё упростить ещё сильнее: каждую перестановку можно записать в виде произведения нескольких транспозиций (это так называются циклы длины 2). Нам по сути достаточно знать, как разложить вот такой цикл:

$$(\begin{array}{ccccc}1& 2& \dots & n-1& n\end{array})=(1n)(1n-1)\dots (13)(12)$$

(Перестановки применяются справа налево, если что.) И тут уже разложение будет неоднозначным, потому что, например, если сделать ротацию большого цикла слева, то получится вот такое:

$$(\begin{array}{ccccc}2& 3& \dots & n& 1\end{array})=(21)(2n)\dots (24)(23)$$

То есть вообще другие транспозиции, совпадают только вот эти $(12)$ в первой и $(21)$ во второй.

---

Знак перестановки

Теорема. Пусть $\pi \in S_n$ и ещё пусть $\pi ={\tau }_1{\tau }_2\dots {\tau }_k$ — произвольное разложение на $k$ транспозиций. Тогда число ${ϵ}_{\pi }=(-1{)}^k$ — это знак перестановки $\pi$ (или сигнатура, чётность). Знак полностью определяется перестановкой и не зависит от выбранного разложения. А ещё взятие знака мультипликативно: ${ϵ}_{\alpha \beta }={ϵ}_{\alpha }{ϵ}_{\beta }$.

Доказательство.

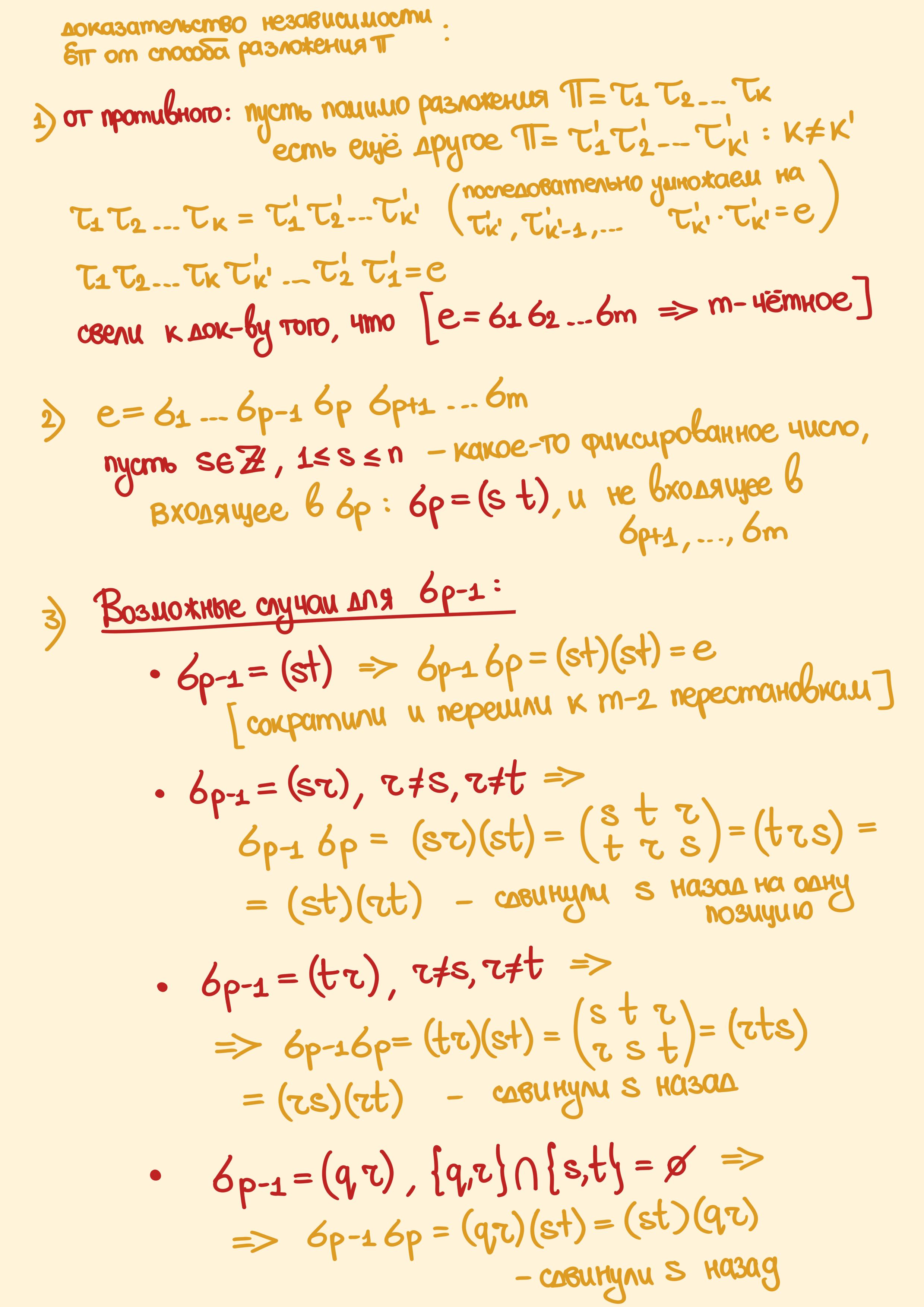
Таким образом, мы постепенно двигаем вот это последнее вхождение числа $s$ влево, пока мы либо не придём к случаю, когда оно сократиться, либо мы доведём $s$ до конца влево, и у нас получится $e={\sigma }_1^{\prime }{\sigma }_2^{\prime }\dots {\sigma }_m^{\prime }$, где ${\sigma }_1^{\prime }=(s{t}^{\prime })$. И вот это $s$ есть только в первой транспозиции, в остальных её нет. Вот в этом втором случае тогда получается противоречие из-за того, что $s$ должно было отобразиться само в себя, потому что:

$$s=e(s)=({\sigma }_1^{\prime }{\sigma }_2^{\prime }\dots {\sigma }_m)(s)={\sigma }_1^{\prime }(s)=t^{\prime }\ne s$$

Так что мы постепенно протаскиваем числа влево $s$ и они сокращаются до того, как достигают самой левой транспозиции, при этом количество траснпозиций уменьшается на 2. Если предположить, что $m$ изначально нечётно, то мы можем такими сокращениями сократить его до единицы, так что получится, что ${\sigma }_1^{\prime }=e$, а это невозможно. Поэтому $m$ чётно, а значит, $k$ и $k^{\prime }$ имеют одинаковую чётность, что доказывает инвариантность знака перестановки вне зависимости от её разложения.

А мультипликативность просто следует из того, что если вот $\alpha ={\tau }_1\dots {\tau }_k$ и $\beta ={\tau }_{k+1}\dots {\tau }_{k+l}$, тогда $\alpha \beta ={\tau }_1\dots {\tau }_{k+l}$. Ну и просто очевидно:

$${ϵ}_{\alpha \beta }=(-1{)}^{k+l}=(-1{)}^k(-1{)}^l={ϵ}_{\alpha }{ϵ}_{\beta }$$

Очевидное следствие из всего этого — это то, что если у нас есть какая-то перестановка $\pi :\mathrm{\Omega }\to \mathrm{\Omega }$ с орбитами ${\mathrm{\Omega }}_1,\dots ,{\mathrm{\Omega }}_n$, то её знак/сигнатура/чётность вычисляется по формуле:

$${ϵ}_{\pi }=(-1{)}^{\Vert {\mathrm{\Omega }}_1\Vert -1}\dots (-1{)}^{\Vert {\mathrm{\Omega }}_n\Vert -1}=(-1{)}^{\sum _{k=1}^n(\Vert {\mathrm{\Omega }}_k\Vert -1)}$$

Потому что каждому циклу соответствует одна орбита, и каждый вот этот цикл разбивается на $|{\mathrm{\Omega }}_k|-1$ транспозиций.

Множества чётных и нечётных перестановок. Таким образом, все перестановки делятся на чётные и нечётные:

$$\begin{gathered} A_n=\{\pi \in S_n\mid {ϵ}_{\pi }=1\}\text{ - чётные перестановки} \\ {S}_n=A_n\cup \overline{A_n} \end{gathered}$$

Перестановки множества перестановок. Можно взять отображение $L_{\tau }:\pi \mapsto \tau \pi$, где $\tau$ — это какая-то произвольная транспозиция. Это отображение будет биективным (оно инъективно, потому что $\tau \alpha =\tau \beta ⟹{\tau }^{-1}\tau \alpha ={\tau }^{-1}\tau \beta ⟹\alpha =\beta$, а сюръективность следует из инъективности и того, что это отображение конечного множества из себя в себя).

Ещё это видно из того, что $L_{\tau }^2$ — это единичное отображение, потому что $L_{\tau }^2:\pi \mapsto \tau \tau \pi =\pi$, так что из этого следует, что $L_{\tau }^{-1}=L_{\tau }$, ну, а так как есть обратное отображение, то это биекция.

Аналогичным образом можно определить $R_{\tau }:\pi \mapsto \pi \tau$, и оно тоже будет биективным. Эти два отображения создают две разных перестановки на $S_n$, и, видимо, пока что они бесполезны, но где-то потом будет использоваться в других местах.

Мощности множеств чётных/нечётных перестановок. ${ϵ}_{\tau \pi }={ϵ}_{\tau }{ϵ}_{\pi }=-{ϵ}_{\pi }$, то есть из чётной перестановки можно сделать нечётную, умножив её ровно на одну любую транспозицию. Поэтому введённые функции $L_{\tau }$ и $R_{\tau }$ переводят нечётные перестановки в чётные и наоборот. В частности: $L_{\tau }(A_n)=\overline{A_n}$, из чего в силу биективности этого отображения следует, что $|A_n|=|\overline{A_n}|=n!/2$.

---

Действие Sn на функциях

Альтернативные определения и выводы для чётности перестановки. Теорему про чётность перестановок можно сформулировать иначе, не используя вот это разбиение на транспозиции, а через понятие инверсий. (Ну, количество инверсий — это количество пар элементов, которые будут стоять не по порядку после применения перестановки. И чётность определяется как чётность количества инверсий. И там точно так же получается, что чётных перестановок столько же, сколько и нечётных, и вообще эти классы совпадают с теми, которые мы определили через транспозиции.)

А ещё можно доказать теорему про чётность перестановок, опираясь на понятие кососимметрической функции. Определим действие перестановки $\pi \in S_n$ на функцию $f$ от каких-то $n$ аргументов как $(\pi \circ f)(x_1,\dots ,x_n):=f(x_{{\pi }_1},\dots ,x_{{\pi }_n})$. То есть аргументы просто перемешиваются.

Действие перестановок на $f$ обладает свойством ассоциативности: $(\alpha \beta )\circ f=\alpha \circ (\beta \circ f)$. Ето довольно просто выводится, если просто по определению подставить, и там всё должно получиться, потому что само перемножение перестановок ассоциативно.

Функция называется кососимметрической, если при перестановке любых её двух соседних аргументов, она меняет знак на противоположный: $f(\dots ,x_k,x_{k+1},\dots )=-f(\dots ,x_{k+1},x_k,\dots )$. Из этого следует, что при перестановке вообще любых двух аргументов кососимметрическая функция поменяет свой знак на противоположный. Например, если мы хотим поменять местами $i$-ый и $j$-ый по счёту аргументы в функции $f(\dots ,x_i,x_{i+1},\dots ,x_{j-1},x_j,\dots )$, то для начала нам надо продвигуть $i$-ый аргумент вправо за $(j-i)$ обменов, после чего сдвинуть $j$-ый за $(j-i-1)$ обменов. Таким образом, суммарно получается $(2(j-i)-1)$ обмен, количество нечётное, каждый обмен меняет знак функции на противоположный, так что выходит, что знак в итоге поменяется на минус.

Один из примеров ненулевой кососимметрической функции — это вот такое: ${\mathrm{\Delta }}_n={\mathrm{\Delta }}_n(x_1,x_2,\dots ,x_n)={\mathrm{\Pi }}_{1\le j<i\le n}(x_i-x_j)$. Короче, произведение всех возможных разностей аргументов без повторений с точностью до порядка разностей. При перестановке местами двух множителей скобка $(x_{k+1}-x_k)$ точно поменяет свой знак на противоположный, а вот в остальном на каждую скобку, которая включает в себя $x_k$ найдётся такая же скобка, но с $x_{k+1}$ вместо $x_k$, так что в остальном набор скобок останется тем же, а значит, знак функции после перестановки $x_k$ и $x_{k+1}$ изменится на противоположный. И эта функция точно не тождественна нулю, короче, доказали, что кососимметрические функции существуют там какие-то.

Теперь с помощью этих кососимметрических функций можно доказать теорему о том, что чётность перестановки не зависит от разложения и что ${ϵ}_{\alpha \beta }={ϵ}_{\alpha }{ϵ}_{\beta }$. Если взять какую-нибудь ненулевую кососимметрическую функцию (а такая существует, как мы только что по няли) и применить к ней перестановку $\pi ={\tau }_1{\tau }_2\dots {\tau }_k$, раскладывающуюся в произведение транспозиций, то:

$$\pi \circ f=({\tau }_1\dots {\tau }_{k-1})\circ ({\tau }_k\circ f)=(-1)({\tau }_1\dots {\tau }_{k-1})\circ f=\cdots =(-1{)}^{k}f={ϵ}_{\pi }f$$

И так получается, что правая часть всего этого по сути не зависит от от разложения, левая — тоже не зависит, значит, ${ϵ}_{\pi }$ не зависит от конкретного разложения $\pi$ на транспозиции. Тут только стоит помнить о том, что будь $f$ нулевой, то ничего бы не вышло, потому что тогда бы значение справа зависело только от нулёвости функции, и нам бы это ни о чём не говорило.

Кстати, вот такое из этого следует доказательство той формулы про чётность произведения перестановок:

$${ϵ}_{\alpha \beta }=(\alpha \beta )\circ f=\alpha \circ (\beta \circ f)=\alpha \circ ({ϵ}_{\beta }f)={ϵ}_{\beta }(\alpha \circ f)=({ϵ}_{\alpha }{ϵ}_{\beta })f$$

Оглавление

• Отображения
  • Ассоциативность композиции отображений
  • Свойства обратных отображений. Отображение обратное композиции
  • Принцип Дирихле в терминах отображений. Отображения объединения и пересечения множеств
• Отношения эквивалентности. Факторизация отображений
  • Бинарные отношения. Отношения эквивалентности
  • Упорядоченные множества

Отображения

---

1.5 в первом томе кострикина

ассоциативность композиции отображений, сюръективность левого обратного, инъективность правого обратного, биективность обратного, обратное отображение для композиции, принцип Дирихле в терминах отображений конечного множества самого в себя, отображение объединения и пересечения множеств

---

Ассоциативность композиции отображений

Теорема 1. Композиция отображений подчиняется закону ассоциативности, то есть:

$$\begin{gathered} \begin{array}{ccc}h:U\to V& g:V\to W& f:W\to T\end{array} \\ ⟹f(gh)=(fg)h \end{gathered}$$

Доказательство. Для базового случая, на самом деле, тут достаточно посмотреть на диаграмму:

Ну и просто, для любой точки $u\in U$ будет выполняться вот это:

$$(f(gh))(u)=f(gh(u))=f(g(h(u)))=fg(h(u))=((fg)h)(u)$$

А для произвольного числа композиций отображений доказывается индукцией. По сути надо только увидеть, что $(f_1{f}_2\dots f_n)f_{n+1}=f_1(f_2\dots f_n{f}_{n+1})$ в индукционном переходе, и это будет означать, что можно ставить скобки как угодно.

---

Свойства обратных отображений. Отображение обратное композиции

Лемма. Если нам даны такие отображения $f:X\to Y$ и $g:Y\to X$, что для них $gf=e_X$, то $f$ — инъекция, а $g$ — сюръекция.

Доказательство. Возьмём $x_1,x_2\in X$ и предположим, что $f(x_1)=f(x_2)$. Тогда:

$$x_1=e_X(x_1)=gf(x_1)=g(f(x_1))=g(f(x_2))=gf(x_2)=x_2$$

Из чего следует инъективность отображения $f$. Сюръективность же $g$ следует из того, что какой бы $x\in X$ мы бы ни взяли, $g(fx)=e_X(x)=x$.

Из этой леммы следует то, что отображение имеет обратное к себе тогда и только тогда, когда оно является биективным. Например, если $g=f^{-1}$ и подставить в предыдущую лемму, то выходит, что $f$ — и инъекция, и сюръекция (потому что $fg=e_Y,gf=e_X$). А обратное утверждение следует просто из того, что так как биективное отображение $f:X\to Y$ сопоставляет каждому элементу из $Y$ единственный элемент из $X$, то можно определить обратное отображение, которое просто будет делать такие же отображения, но в обратную сторону.

А ещё есть вот такое свойство отображения, обратного композиции отображений:

$$\begin{gathered} \begin{array}{cc}f:X\to Y& g:Y\to Z\end{array} \\ (gf)(f^{-1}{g}^{-1})=g(f{f}^{-1})h=g{g}^{-1}=e_Y \\ (f^{-1}{g}^{-1})(gf)=f^{-1}(g^{-1}g)f=f^{-1}f=e_Z \end{gathered}$$

То есть, $(gf{)}^{-1}=f^{-1}{g}^{-1}$.

---

Принцип Дирихле в терминах отображений. Отображения объединения и пересечения множеств

Тут ещё он рассказывает про то, что инъективное отображение конечного множества самого в себя будет биективным. И аналогично с сюръективным отображением. По сути это же следует из принципа Дирихле:

• Если кролики рассажены в клетки, кроликов столько же, сколько и клеток, и ни в одной из клеток не сидит больше одного кролика, то в каждой клетке есть по крайней мере один кролик.
• Если в каждой клетке есть хотя бы один кролик и клеток столько же, сколько кроликов, то в каждой клетке сидит ровно один кролик.

Ну и ещё вот та кой прикол есть: если $A\subset B$, то и $f(A)\subset f(B)$. Это доказывается методом от противного: предположим, что это не так, то есть $\mathrm{\exists }t\in f(A):t\notin f(B)$. Но тогда, если $t=f(a),a\in A$, то из этого следует, что $a\notin B$, а это противоречит условию. На этом основываются ещё вот такая штука:

$$\begin{gathered} A\cap B\subset A \\ \begin{array}{cc}f(A\cap B)\subset f(A)& f(A\cap B)\subset f(B)\end{array} \\ ⟹f(A\cap B)\subset f(A)\cap f(B) \end{gathered}$$

И аналогично выводится вот такая штука:

$$\begin{array}{}\begin{array}{cc}A\subset A\cup B& B\subset A\cup B\end{array}⟹f(A)\cup f(B)\subset f(A\cup B)\\ f(A\cup B)\subset f(A)\cup f(B)\end{array}\}⟹f(A\cup B)=f(A)\cup f(B)$$

Отношения эквивалентности. Факторизация отображений

---

1.6 в первом томе кострикина

бинарные отношения, график отображения, отношения эквивалентности, классы эквивалентности, фактиоризация, упорядоченные множества, накрытие и сравнимость, наибольший и максимальный элементы в частично упорядоченном множестве

---

Бинарные отношения. Отношения эквивалентности

Для любых двух множеств $X$ и $Y$ любое подмножество $\omega \subset X\times Y$ называется бинарным отношением между $X$ и $Y$ (или же, если $Y=X$, то это просто отношение на $X$).

$\mathrm{\Gamma }(f)=(x,y)\mid x\in X,y=f(x)\subset X\times Y$ — это просто график бинарного отношения или же функции $f:X\to Y$. Ну, просто, да, что тут ещё можно ожидать.

Бинарное отношение $\sim$ на $X$ называется отношением эквивалентности, если выполняются условия:

• $a\sim a$ — рефлексивность.
• $a\sim b⟹b\sim a$ — симметричность.
• $a\sim b,b\sim c⟹a\sim c$ — транзитивность.

Отношение эквивалентности разбивает множество на классы эквивалентности $\bar{x}=x^{\prime }\in X\mid x^{\prime }\sim x$ (различные классы не пересекаются, потому что, если предположить обратное, то из-за транзитивности получится, что пересекающиеся классы совпадают, и все они суммарно составляют множество $X$). И обратное тоже верно: если есть какое-то разбиение множества, то ему соответствует отношение эквивалентности.

$X/\sim$ — это фактормножество $X$ относительно $\sim$. По сути это просто множество всех классов эквивалентности. Отображение $p:x\to p(x)=\bar{x}$, сопоставляющее каждому элементу множества его класс эквивалетности, называется естественным отображением или канонической проекцией.

В качестве примера рассмотрим отображение $f:X\to Y$. Определим отношение на множестве $X$ следующим образом: $x\sim x^{\prime }⟺f(x)=f(x^{\prime })$. Это будет отношением эквивалентности, достаточно проверить выполнение всех трёх свойств. Классы эквивалентности в этом случае являются слоями отображения, а отношение эквивалентности индуцирует отображение $\bar{f}:X/\sim \to Y$, которое отображает класс эквивалентности в соответствующее значение функции. При этом тут говорят, что $\bar{f}$ хорошо определена, так как её значение не зависит от выбора представителя класса в качестве аргумента.

---

Упорядоченные множества

Упорядочением множества $X$ (порядком на множестве $X$) называется бинарное отношение $\le$ на $X$, которое обладает следующими свойствами:

• $x\le x$ — рефлексивность.
• $x\le y,y\le x⟹x=y$ — антисимметричность.
• $x\le y,y\le z⟹x\le z$ — транзитивность.

Если все элементы множества сравнимы друг с другом, то говорят, что множество линейно упорядочено. Иначе в общем случае говорят о частичном порядке на $X$.

Говорят, что $y\in X$ накрывает $x\in X$, если $x\le y$ и не существует такого $z\in X$, который может встать между ними: $x\le z\le y$. В случае с конечным множеством $|X|<\mathrm{\infty }$, $x$ и $y$ сравнимы тогда и только тогда, когда существует конечная цепочка $x=x_1,x_2,\dots ,x_n=y$, в которой $x_{i+1}$ накрывает $x_i$.

Накрытия можно изобразить в виде диаграмм, в которых верхние элементы накрывают нижние. В итоге получается так, что сравнимые элементы соединяются линиями, идущими сверху вниз. Между несравнимыми элементами линий нет.

Наибольшим элементом частично упорядоченного множества $X$ называется такой $n\in X$, что $x\le n,\mathrm{\forall }x\in X$. В силу антисимметричности существует ровно один наибольший элемент. А есть ещё максимальный элемент — это такой элемент $m\in X$, для которого из неравенства $m\le x\in X$ следует $x=m$. Очевидно, наибольший элемент всегда является максимальным. Но обратное не верно в общем случае. Да и вообще максимальных элементов может быть несколько: например, в диаграмме на картинке ниже наибольшего элемента нет, потому что просто нет такого элемента, который был бы сравним со всеми остальными. Но зато есть три максимальных.

Аналогичные определения можно дать для наименьшего элемента и минимального элемента. О минимальных и максимальных элементах можно думать как о локальных минимумах/максимумах.