Оглавление
Linear Algebra 2
Перестановки
1.8 в первом томе кострикина
перестановки, симметрическая группа, циклическая запись перестановок, порядок перестановки, орбиты, длина орбиты, единственность разложения на циклы, разложение на транспозиции (циклы длины 2), знак (чётность) перестановки, независимость чётности перестановки от разложения, чётность произведения перестановок, формула для определения чётности, перестановка перестановок
действие перестановок на функции, кососимметрические функции (с примером), доказательство независимости чётности перестановки от разложения через кососимметрические функции
Перестановки
Перестановкой называется биективное отображение конечного множества $\Omega = {1,2,\dots,n}$ (сами элементы не важны, поэтому просто для удобства обозначим их циферками) самого на себя. Это отображение $\pi:\,i \rightarrow \pi(i)$ можно ещё записать вот в такой форме:
\[\pi = \left(\begin{matrix} 1 & 2 & \dots & n \\ i_1 & i_2 & \dots & i_n \end{matrix}\right)\]Сверху записаны элементы множества $\Omega$, а снизу записано то, куда каждый из них отображается: $\pi(k) = i_k$. Ну, это такая, дефолтная запись перестановки, с помощью которой в том числе удобно перемножать перестановки:
\[\sigma\tau = \left(\begin{matrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \end{matrix}\right) \left(\begin{matrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{matrix}\right) = \begin{matrix} 1 & 2 & 3 & 4 \\ \downarrow & \downarrow & \downarrow &\downarrow \\ 4 & 3 & 2 & 1 \\ \downarrow & \downarrow & \downarrow &\downarrow \\ 1 & 4 & 3 & 2 \end{matrix} = \left(\begin{matrix} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \end{matrix}\right)\]Так как множество перестановок $S_n$ обладает свойствами ассоциативности, есть единичный элемент (перестановка, которая каждый элемент отображает сам в себя) и для каждого есть обратная перестановка, то $S_n$ образуют группу, которая называется симметрической группой степени n. $|S_n| = n!$ — ну это как бы да, очевидно.
Циклическая структура перестановки
Перестановки можно раскладывать в произведение нескольких более простых перестановок. Получается более удобная и при кольная запись. Например, если перестановка имеет вид $\pi(i) \rightarrow (i \mod 4)+1$, то её можно записать в виде $\sigma = (1 \,\, 2 \,\, 3 \,\, 4)$: здесь числа переводятся в те, которые следуют за ними, и предполагается, что эта штука циклически замкнута. Перестановка может состоять и из нескольких непересекающихся циклов: $\tau = (1\,\,4)(2\,\,3)$. Так что получается, что $\sigma^4 = e$ и $\tau^2 = e$ — если возвести в наименьшее общее кратное длин циклов перестановки, получим единичную перестановку. Очевидно, то вот эти циклические штуки можно записывать с разными ротациями, это сути не меняет.
Возведение перестановки в степень. Так как перестановка — это биективное отображение из конечного множества в конечное, то обязательно найдётся такая степень $\pi^k = \pi(\pi\dots \pi (i))$, что $\pi^k = e$. Множество конечно, значит, найдутся такие $m$ и $n$, $m > n$, что $\pi^m (i) = \pi^n(i),\, \forall i \in \Omega$, потому что существует конечное число способов отобразить $\Omega$ само в себя. $\pi(\pi^{m-1}(i)) = \pi(\pi^{n-1}(i))$, и в силу инъективности (на самом деле, тут достаточно только её, сюръективность следует из всего этого) по значению функции можно однозначно определить соответствующий аргумент, так что можно сократить: $\pi^{m-1}(i) = \pi^{n-1}(i)$. И так сокращаем до упора и получаем $\pi^{m-n}(i) = e(i)$.
Кстати, это же самое работает и для любой инъективной функции на конечном множестве, и из последнего вывода следовала бы её сюръективность, потому что $\pi(\pi^{m-n-1}) = e$, то есть любому значению $i \in \Omega$ соответствует аргумент $\pi^{m-n-1}(i)$.
Степень перестановки, кстати, определяется индуктивно вот так:
\[\pi^s = \begin{cases} \pi(\pi^{s-1}), & \text{если } s \gt 0,\\ e, & \text{если } s = 0,\\ \pi^{-1}((\pi^{-1})^{-s-1}), & \text{если } s \lt 0. \end{cases}\](Короче, просто, если степень положительная, то это несколько умножений $\pi$ самого на себя, если отрицательная — то это несколько умножений $\pi^{-1}$ самого на себя. Я не знаю, зачем я написал это, просто я сначала чего-то совсем не понял, что имеется в виду в этой формуле.)
Порядком перестановки называется такое наименьшее число $q \in \mathbb{Z}_{>0}$, что $\pi^q = e$ (ну и, соответственно, получится так, что все различные степени будут содержаться в множестве ${e, \pi,\dots,\pi^{q-1}}$).
Эквивалентные точки. Назовём две точки $i,\,j \in \Omega$ $\pi$-эквивалентными, если $j = \pi^s(i)$ для некоторого $s \in \mathbb{Z}$. Это будет отношением эквивалентности, так как, очевидно, любая точка эквивалентна сама себе ($\pi^0 = e$), это отношение симметрично и транзитивно. Так что перестановка разбивает множество $\Omega$ на несколько классов экивалентности, которые называются $\pi$-орбитами: $\Omega = \Omega_1 \cup \dots \cup \Omega_p$. Количество элементов в классе эквивалентности — это длина орбиты. Если у нас есть элемент орбиты, то все остальные можно найти, последовательно применяя к нему перестановку.
Определение циклов перестановки. Каждой орбите можно сопоставить цикл длины $l_k = |\Omega_k|$, который определяется вот так:
\[\pi_k := (\begin{matrix}i & \pi(i) & \dots & \pi^{l_k-1}(i)\end{matrix})\]То есть получается перестановка, которая применяет ко всем элементам $i \in \Omega \setminus \Omega_k$ перестановку $\pi$. Так что любая перестановка разбивается на такие независимые циклы: $\pi = \pi_1 \pi_2 \dots \pi_p$. При этом не имеет значения, в каком порядке они расположены, потому что они друг от друга не зависят. При этом в записи естественно опускать циклы длины 1.
Единственность разложения на циклы.

При этом можно всё упростить ещё сильнее: каждую перестановку можно записать в виде произведения нескольких транспозиций (это так называются циклы длины 2). Нам по сути достаточно знать, как разложить вот такой цикл:
\[(\begin{matrix}1 & 2 & \dots & n-1 & n\end{matrix}) = (1 \,\, n) (1 \,\, n-1) \dots (1 \,\, 3) (1 \,\, 2)\](Перестановки применяются справа налево, если что.) И тут уже разложение будет неоднозначным, потому что, например, если сделать ротацию большого цикла слева, то получится вот такое:
\[(\begin{matrix}2 & 3 & \dots & n & 1\end{matrix}) = (2 \,\, 1) (2 \,\, n) \dots (2 \,\, 4) (2 \,\, 3)\]То есть вообще другие транспозиции, совпадают только вот эти $(1\,\,2)$ в первой и $(2\,\,1)$ во второй.
Знак перестановки
Теорема. Пусть $\pi \in S_n$ и ещё пусть $\pi = \tau_1 \tau_2 \dots \tau_k$ — произвольное разложение на $k$ транспозиций. Тогда число $\epsilon_\pi = (-1)^k$ — это знак перестановки $\pi$ (или сигнатура, чётность). Знак полностью определяется перестановкой и не зависит от выбранного разложения. А ещё взятие знака мультипликативно: $\epsilon_{\alpha\beta} = \epsilon_{\alpha} \epsilon_{\beta}$.
Доказательство.
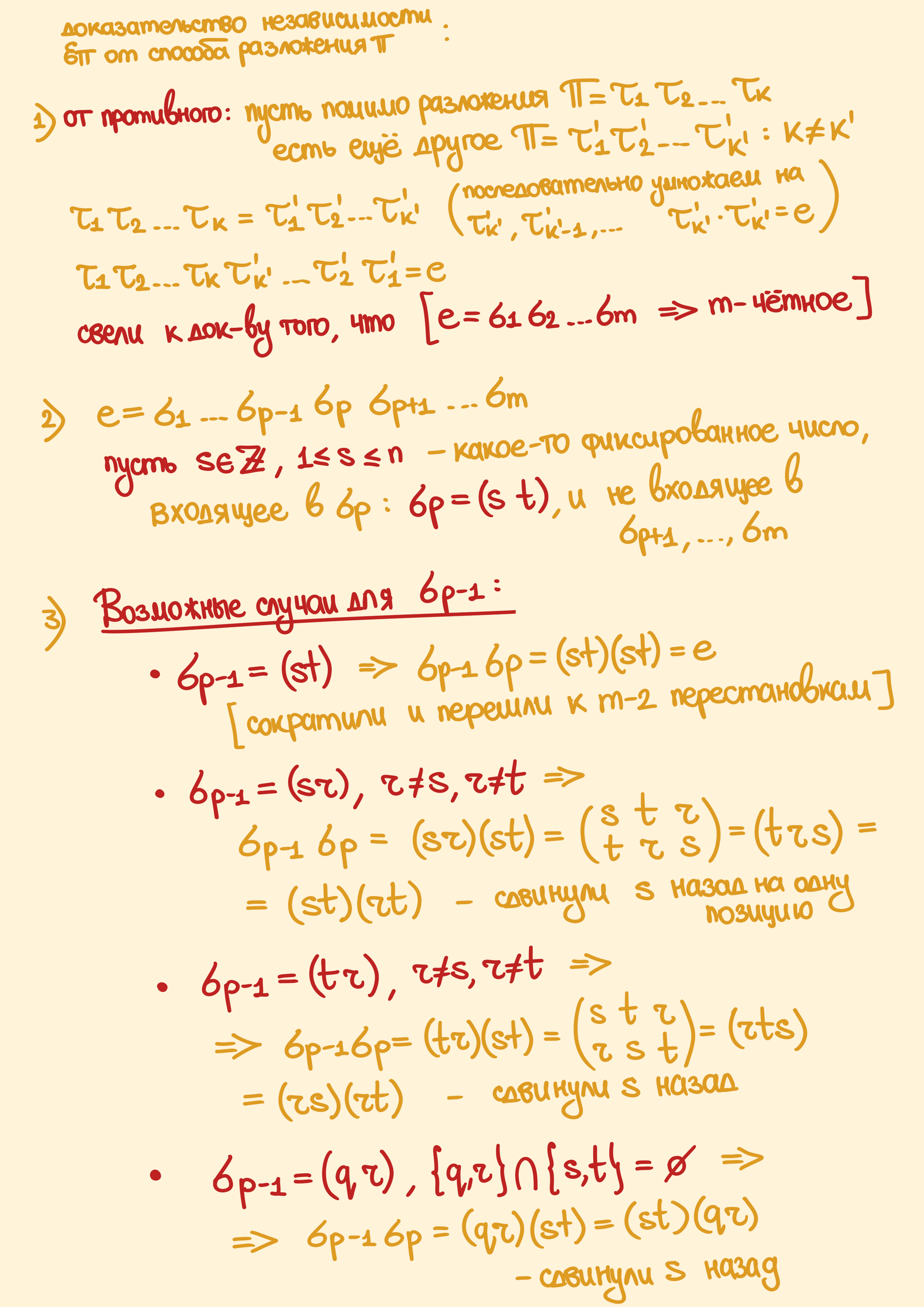
Таким образом, мы постепенно двигаем вот это последнее вхождение числа $s$ влево, пока мы либо не придём к случаю, когда оно сократиться, либо мы доведём $s$ до конца влево, и у нас получится $e = \sigma_1’ \sigma_2’ \dots \sigma_m’$, где $\sigma_1’ = (s \,\, t’)$. И вот это $s$ есть только в первой транспозиции, в остальных её нет. Вот в этом втором случае тогда получается противоречие из-за того, что $s$ должно было отобразиться само в себя, потому что:
\[s = e(s) = (\sigma_1' \sigma_2' \dots \sigma_m)(s) = \sigma_1'(s) = t' \not = s\]Так что мы постепенно протаскиваем числа влево $s$ и они сокращаются до того, как достигают самой левой транспозиции, при этом количество траснпозиций уменьшается на 2. Если предположить, что $m$ изначально нечётно, то мы можем такими сокращениями сократить его до единицы, так что получится, что $\sigma_1’ = e$, а это невозможно. Поэтому $m$ чётно, а значит, $k$ и $k’$ имеют одинаковую чётность, что доказывает инвариантность знака перестановки вне зависимости от её разложения.
А мультипликативность просто следует из того, что если вот $\alpha = \tau_1 \dots \tau_k$ и $\beta = \tau_{k+1}\dots \tau_{k + l}$, тогда $\alpha\beta = \tau_1 \dots \tau_{k + l}$. Ну и просто очевидно:
\[\epsilon_{\alpha\beta} = (-1)^{k + l} = (-1)^k (-1)^l = \epsilon_\alpha \epsilon_\beta\]Очевидное следствие из всего этого — это то, что если у нас есть какая-то перестановка $\pi:\,\Omega \rightarrow \Omega$ с орбитами $\Omega_1, …, \Omega_n$, то её знак/сигнатура/чётность вычисляется по формуле:
\[\epsilon_\pi = (-1)^{\|\Omega_1\| - 1} \dots (-1)^{\|\Omega_n\| - 1} = (-1)^{\sum_{k=1}^n(\|\Omega_k\| - 1)}\]Потому что каждому циклу соответствует одна орбита, и каждый вот этот цикл разбивается на $|\Omega_k| - 1$ транспозиций.
Множества чётных и нечётных перестановок. Таким образом, все перестановки делятся на чётные и нечётные:
\[A_n = \{\pi \in S_n \mid \epsilon_\pi = 1\} \text{ - чётные перестановки} \\ S_n = A_n \cup \overline {A_n}\]Перестановки множества перестановок. Можно взять отображение $L_\tau:\, \pi \mapsto \tau\pi$, где $\tau$ — это какая-то произвольная транспозиция. Это отображение будет биективным (оно инъективно, потому что $\tau \alpha = \tau \beta \implies \tau^{-1} \tau \alpha = \tau^{-1} \tau \beta \implies \alpha = \beta$, а сюръективность следует из инъективности и того, что это отображение конечного множества из себя в себя).
Ещё это видно из того, что $L_\tau^2$ — это единичное отображение, потому что $L_\tau^2:\, \pi \mapsto \tau \tau \pi = \pi$, так что из этого следует, что $L_\tau^{-1} = L_\tau$, ну, а так как есть обратное отображение, то это биекция.
Аналогичным образом можно определить $R_\tau:\,\pi \mapsto \pi \tau$, и оно тоже будет биективным. Эти два отображения создают две разных перестановки на $S_n$, и, видимо, пока что они бесполезны, но где-то потом будет использоваться в других местах.
Мощности множеств чётных/нечётных перестановок. $\epsilon_{\tau \pi} = \epsilon_{\tau} \epsilon_{\pi} = -\epsilon_\pi$, то есть из чётной перестановки можно сделать нечётную, умножив её ровно на одну любую транспозицию. Поэтому введённые функции $L_\tau$ и $R_\tau$ переводят нечётные перестановки в чётные и наоборот. В частности: $L_\tau(A_n) = \overline{A_n}$, из чего в силу биективности этого отображения следует, что $|A_n| = |\overline{A_n}| = n! / 2$.
Действие Sn на функциях
Альтернативные определения и выводы для чётности перестановки. Теорему про чётность перестановок можно сформулировать иначе, не используя вот это разбиение на транспозиции, а через понятие инверсий. (Ну, количество инверсий — это количество пар элементов, которые будут стоять не по порядку после применения перестановки. И чётность определяется как чётность количества инверсий. И там точно так же получается, что чётных перестановок столько же, сколько и нечётных, и вообще эти классы совпадают с теми, которые мы определили через транспозиции.)
А ещё можно доказать теорему про чётность перестановок, опираясь на понятие кососимметрической функции. Определим действие перестановки $\pi \in S_n$ на функцию $f$ от каких-то $n$ аргументов как $(\pi \circ f)(x_1, \dots, x_n) := f(x_{\pi_1}, \dots, x_{\pi_n})$. То есть аргументы просто перемешиваются.
Действие перестановок на $f$ обладает свойством ассоциативности: $(\alpha \beta) \circ f = \alpha\circ(\beta \circ f)$. Ето довольно просто выводится, если просто по определению подставить, и там всё должно получиться, потому что само перемножение перестановок ассоциативно.
Функция называется кососимметрической, если при перестановке любых её двух соседних аргументов, она меняет знак на противоположный: $f(\dots, x_k,x_{k+1},\dots) = -f(\dots, x_{k+1},x_k,\dots)$. Из этого следует, что при перестановке вообще любых двух аргументов кососимметрическая функция поменяет свой знак на противоположный. Например, если мы хотим поменять местами $i$-ый и $j$-ый по счёту аргументы в функции $f(\dots,x_i,x_{i+1},\dots,x_{j-1},x_j, \dots)$, то для начала нам надо продвигуть $i$-ый аргумент вправо за $(j - i)$ обменов, после чего сдвинуть $j$-ый за $(j - i - 1)$ обменов. Таким образом, суммарно получается $(2(j - i) - 1)$ обмен, количество нечётное, каждый обмен меняет знак функции на противоположный, так что выходит, что знак в итоге поменяется на минус.
Один из примеров ненулевой кососимметрической функции — это вот такое: $\Delta_n = \Delta_n(x_1,x_2,\dots,x_n) = \Pi_{1 \leq j \lt i \leq n}(x_i - x_j)$. Короче, произведение всех возможных разностей аргументов без повторений с точностью до порядка разностей. При перестановке местами двух множителей скобка $(x_{k+1} - x_k)$ точно поменяет свой знак на противоположный, а вот в остальном на каждую скобку, которая включает в себя $x_k$ найдётся такая же скобка, но с $x_{k+1}$ вместо $x_k$, так что в остальном набор скобок останется тем же, а значит, знак функции после перестановки $x_k$ и $x_{k+1}$ изменится на противоположный. И эта функция точно не тождественна нулю, короче, доказали, что кососимметрические функции существуют там какие-то.
Теперь с помощью этих кососимметрических функций можно доказать теорему о том, что чётность перестановки не зависит от разложения и что $\epsilon_{\alpha\beta} = \epsilon_{\alpha}\epsilon_\beta$. Если взять какую-нибудь ненулевую кососимметрическую функцию (а такая существует, как мы только что по няли) и применить к ней перестановку $\pi = \tau_1\tau_2\dots\tau_k$, раскладывающуюся в произведение транспозиций, то:
\[\pi \circ f = (\tau_1 \dots \tau_{k-1})\circ(\tau_k \circ f) = (-1)(\tau_1\dots\tau_{k-1})\circ f = \dots = (-1)^kf = \epsilon_\pi f\]И так получается, что правая часть всего этого по сути не зависит от от разложения, левая — тоже не зависит, значит, $\epsilon_\pi$ не зависит от конкретного разложения $\pi$ на транспозиции. Тут только стоит помнить о том, что будь $f$ нулевой, то ничего бы не вышло, потому что тогда бы значение справа зависело только от нулёвости функции, и нам бы это ни о чём не говорило.
Кстати, вот такое из этого следует доказательство той формулы про чётность произведения перестановок:
\[\epsilon_{\alpha\beta} = (\alpha\beta) \circ f = \alpha \circ (\beta \circ f) = \alpha \circ (\epsilon_\beta f) = \epsilon_\beta(\alpha \circ f) = (\epsilon_{\alpha}\epsilon_\beta)f\]