Оглавление

Linear Algebra 1

Отображения

1.5 в первом томе кострикина

ассоциативность композиции отображений, сюръективность левого обратного, инъективность правого обратного, биективность обратного, обратное отображение для композиции, принцип Дирихле в терминах отображений конечного множества самого в себя, отображение объединения и пересечения множеств


Ассоциативность композиции отображений

Теорема 1. Композиция отображений подчиняется закону ассоциативности, то есть:

\[\begin{matrix}h: U \rightarrow V & g: V \rightarrow W & f: W \rightarrow T\end{matrix}\\ \implies f (g h) = (f g) h\]

Доказательство. Для базового случая, на самом деле, тут достаточно посмотреть на диаграмму:

Ну и просто, для любой точки $u \in U$ будет выполняться вот это:

\[(f(gh))(u) = f(gh(u)) = f(g(h(u))) = fg(h(u)) = ((fg)h)(u)\]

А для произвольного числа композиций отображений доказывается индукцией. По сути надо только увидеть, что $(f_1 f_2 \dots f_n) f_{n+1} = f_1 (f_2 \dots f_n f_{n+1})$ в индукционном переходе, и это будет означать, что можно ставить скобки как угодно.


Свойства обратных отображений. Отображение обратное композиции

Лемма. Если нам даны такие отображения $f:X \rightarrow Y$ и $g:Y \rightarrow X$, что для них $gf = e_X$, то $f$ — инъекция, а $g$ — сюръекция.

Доказательство. Возьмём $x_1, x_2 \in X$ и предположим, что $f(x_1) = f(x_2)$. Тогда:

\[x_1 = e_X(x_1) = gf(x_1) = g(f(x_1)) = g(f(x_2)) = gf(x_2) = x_2\]

Из чего следует инъективность отображения $f$. Сюръективность же $g$ следует из того, что какой бы $x \in X$ мы бы ни взяли, $g(fx) = e_X(x) = x$.

Из этой леммы следует то, что отображение имеет обратное к себе тогда и только тогда, когда оно является биективным. Например, если $g=f^{-1}$ и подставить в предыдущую лемму, то выходит, что $f$ — и инъекция, и сюръекция (потому что $fg = e_Y, gf = e_X$). А обратное утверждение следует просто из того, что так как биективное отображение $f: X \rightarrow Y$ сопоставляет каждому элементу из $Y$ единственный элемент из $X$, то можно определить обратное отображение, которое просто будет делать такие же отображения, но в обратную сторону.

А ещё есть вот такое свойство отображения, обратного композиции отображений:

\[\begin{matrix}f:X \rightarrow Y & g: Y \rightarrow Z\end{matrix}\\ (gf)(f^{-1}g^{-1}) = g(ff^{-1})h = gg^{-1} = e_Y\\ (f^{-1}g^{-1})(gf) = f^{-1}(g^{-1}g)f = f^{-1}f = e_Z\]

То есть, $(gf)^{-1} = f^{-1} g^{-1}$.


Принцип Дирихле в терминах отображений. Отображения объединения и пересечения множеств

Тут ещё он рассказывает про то, что инъективное отображение конечного множества самого в себя будет биективным. И аналогично с сюръективным отображением. По сути это же следует из принципа Дирихле:

Ну и ещё вот та кой прикол есть: если $A \subset B$, то и $f(A) \subset f(B)$. Это доказывается методом от противного: предположим, что это не так, то есть $\exists t \in f(A): t \not \in f(B)$. Но тогда, если $t = f(a), a \in A$, то из этого следует, что $a \not \in B$, а это противоречит условию. На этом основываются ещё вот такая штука:

\[A \cap B \subset A \\ \begin{matrix} f(A \cap B) \subset f(A) & f(A \cap B) \subset f(B) \end{matrix} \\ \implies f(A \cap B) \subset f(A) \cap f(B)\]

И аналогично выводится вот такая штука:

\[\left. \begin{array}{1} \begin{matrix} A \subset A \cup B & B \subset A \cup B \end{matrix} \implies f(A) \cup f(B) \subset f(A \cup B) \\ f(A \cup B) \subset f(A) \cup f(B)\\ \end{array} \right\} \implies f(A \cup B) = f(A) \cup f(B)\]



Отношения эквивалентности. Факторизация отображений

1.6 в первом томе кострикина

бинарные отношения, график отображения, отношения эквивалентности, классы эквивалентности, фактиоризация, упорядоченные множества, накрытие и сравнимость, наибольший и максимальный элементы в частично упорядоченном множестве


Бинарные отношения. Отношения эквивалентности

Для любых двух множеств $X$ и $Y$ любое подмножество $\omega \subset X \times Y$ называется бинарным отношением между $X$ и $Y$ (или же, если $Y = X$, то это просто отношение на $X$).

$\Gamma(f) = {(x,y) \mid x \in X,\, y = f(x)} \subset X \times Y$ — это просто график бинарного отношения или же функции $f:\,X \rightarrow Y$. Ну, просто, да, что тут ещё можно ожидать.

Бинарное отношение $\sim$ на $X$ называется отношением эквивалентности, если выполняются условия:

Отношение эквивалентности разбивает множество на классы эквивалентности $\overline x = {x’ \in X \mid x’ \sim x}$ (различные классы не пересекаются, потому что, если предположить обратное, то из-за транзитивности получится, что пересекающиеся классы совпадают, и все они суммарно составляют множество $X$). И обратное тоже верно: если есть какое-то разбиение множества, то ему соответствует отношение эквивалентности.

$X/\sim$ — это фактормножество $X$ относительно $\sim$. По сути это просто множество всех классов эквивалентности. Отображение $p:\,x \rightarrow p(x) = \overline x$, сопоставляющее каждому элементу множества его класс эквивалетности, называется естественным отображением или канонической проекцией.

В качестве примера рассмотрим отображение $f:\, X \rightarrow Y$. Определим отношение на множестве $X$ следующим образом: $x \sim x’ \iff f(x) = f(x’)$. Это будет отношением эквивалентности, достаточно проверить выполнение всех трёх свойств. Классы эквивалентности в этом случае являются слоями отображения, а отношение эквивалентности индуцирует отображение $\overline f:\, X/\sim\, \rightarrow Y$, которое отображает класс эквивалентности в соответствующее значение функции. При этом тут говорят, что $\overline{f}$ хорошо определена, так как её значение не зависит от выбора представителя класса в качестве аргумента.


Упорядоченные множества

Упорядочением множества $X$ (порядком на множестве $X$) называется бинарное отношение $\leq$ на $X$, которое обладает следующими свойствами:

Если все элементы множества сравнимы друг с другом, то говорят, что множество линейно упорядочено. Иначе в общем случае говорят о частичном порядке на $X$.

Говорят, что $y \in X$ накрывает $x \in X$, если $x \leq y$ и не существует такого $z \in X$, который может встать между ними: $x \leq z \leq y$. В случае с конечным множеством $| X | \lt \infty$, $x$ и $y$ сравнимы тогда и только тогда, когда существует конечная цепочка $x = x_1,x_2,\dots,x_n = y$, в которой $x_{i+1}$ накрывает $x_i$.

Накрытия можно изобразить в виде диаграмм, в которых верхние элементы накрывают нижние. В итоге получается так, что сравнимые элементы соединяются линиями, идущими сверху вниз. Между несравнимыми элементами линий нет.

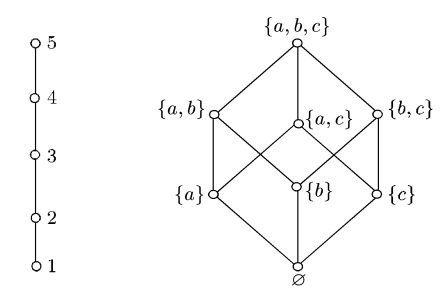
image-20200330180309314

Наибольшим элементом частично упорядоченного множества $X$ называется такой $n \in X$, что $x \leq n,\,\forall x \in X$. В силу антисимметричности существует ровно один наибольший элемент. А есть ещё максимальный элемент — это такой элемент $m \in X$, для которого из неравенства $m \leq x \in X$ следует $x = m$. Очевидно, наибольший элемент всегда является максимальным. Но обратное не верно в общем случае. Да и вообще максимальных элементов может быть несколько: например, в диаграмме на картинке ниже наибольшего элемента нет, потому что просто нет такого элемента, который был бы сравним со всеми остальными. Но зато есть три максимальных.

Аналогичные определения можно дать для наименьшего элемента и минимального элемента. О минимальных и максимальных элементах можно думать как о локальных минимумах/максимумах.