Оглавление

• The geometry of linear equations
• Системы линейных уравнений (2–3 порядков)
  • Терминология
  • Эквивалентность линейных систем
  • Приведение к ступенчатому виду
  • Некоторые при кольные замечания
  • Определители небольших порядков

The geometry of linear equations

ссылка — там вообще ничего интересного

Система линейных уравнений: \(\begin{cases} a_1 x + b_1 y = c_1 \\ a_2 x + b_2 y = c_1\end{cases}\)

Её можно проинтерпретировать двумя способами:

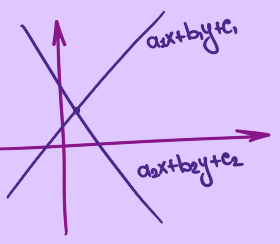
• row picture

  \[\left(\begin{matrix} a_1 & b_1\\ a_2 & b_2 \end{matrix}\right) \cdot \left(\begin{matrix} x \\ y \end{matrix}\right) = \left(\begin{matrix} c_1 \\ c_2 \end{matrix}\right)\] \[Ax = b\]

  Эту систему уравнений можно также представить как пересечение двух прямых. В случае с тремя линейными уравнениями мы имели бы дело с тремя плоскостями, и дальше уже всё становится совсем плохо. Короче, это не очень наглядный вариант.

  

• column picture

  \[x \cdot \left(\begin{matrix} a_1 \\ a_2 \end{matrix}\right) + y \cdot \left(\begin{matrix} b_1 \\ b_2 \end{matrix}\right) = \left(\begin{matrix} c_1 \\ c_2 \end{matrix}\right)\]

  В этом случае система представляется как линейная комбинация векторов, которая равна какому-то другому вектору. То есть решение сводится к тому, что нужно определить, сколько нужно взять от первого вектора и сколько от второго, чтобы в сумме получился $\left(\begin{matrix}c1 \ c2\end{matrix}\right)$.

  

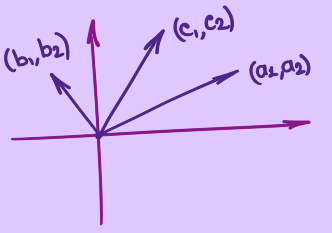
Один из вопросов, который ставится в линейной алгебре: Можно ли решить уравнение $Ax = b$ для любого $b$? Его же можно поставить другим образом: Заполняют ли всё пространство линейные комбинации двух данных векторов? Очевидно, что ответ на этот вопрос не всегда положительный: например, для случая с тремя уравнениями, если все три вектора лежат в одной плоскости.

По аналогии с row/column picture произведение матрицы на вектор можно представлять как два dot-product’а, а можно, как линейную комбинацию двух векторов:

\[\left(\begin{matrix} a_1 & b_1\\ a_2 & b_2 \end{matrix}\right) \cdot \left(\begin{matrix} x \\ y \end{matrix}\right) = \left(\begin{matrix} a_1 \\ a_2 \end{matrix}\right) \cdot x + \left(\begin{matrix} b_1 \\ b_2 \end{matrix}\right) \cdot y\]

Системы линейных уравнений (2–3 порядков)

1.1–1.4 в первом томе кострикина

Терминология

Общий вид системы линейных алгебраических уравнений:

\[\begin{cases} a_{11} x_1 + a_{12} x_2 + \ldots + a_{1n} x_n = b_1 \\ a_{21} x_1 + a_{22} x_2 + \ldots + a_{2n} x_n = b_2 \\ \ldots \\ a_{m1} x_1 + a_{m2} x_2 + \ldots + a_{mn} x_n = b_m \\ \end{cases} (1)\]

Такая система называется однородной, если все свободные члены (все $b_i$) равны нулю. Система, аналогичная системе $(1)$, но с обнулёнными свободными членами называется приведённой системой.

Система, не имеющая ни одного решения, называется несовместной, иначе — называется совместной. Если решение единственное, то система называется определённой, если же решений несколько или ни одного, то система называется неопределённой.

Эквивалентность линейных систем

• Элементарное преобразование типа (I) — когда меняем в системе два уравнения местами

• Элементарное преобразование типа (II) — это, когда берём в системе какое-то уравнение, домножаем его на какое-то число, и прибавляем всё это к какому-то другому уравнению, так что получается что-то вроде:

  \[(a_{i1} + c a_{k1}) x_1 + \ldots + (a_{in} + c a_{kn}) x_n = b_i + c b_k\]

Будем говорить, что две линейные системы называются эквивалентными, если обе они либо несовместны, либо совместны и их решения совпадают.

Теорема 1: Две линейные системы эквивалентны, если одна получается из другой путём применения конечной последовательности элементарных преобразований.

Доказательство: Если доказать, что после применения любого из элементарных преобразований получается эквивалентная система, то из этого будет следовать, что после любой последовательности элементарных преобразований получится эквивалентная система. А ещё можно доказывать теорему только в одну сторону, потому что элементарные преобразования обратимы: нужно только доказать, что любое решение первой системы является также решением второй (а это очевидно, мне лень писать).

Приведение к ступенчатому виду

Путём элементарных преобразований можно привести систему уравнений к более простому виду:

1. Найдём уравнение, у которого бы первый коэффициент $a_{i1}$ был ненулевым (если такого нет, то переменная $x_1$ может принимать любое значение, можно забить на неё и перейти к следующей).

2. Ставим это уравнение первым в системе, и прибавляем его ко всем остальным, домножив на такой коэффициент, чтобы во всех остальных уравнениях первый коэффициент обнулился.

3. Повторяем всё то же самое для оставшихся уравнений, пока не получим уравнение вида:

   \[\begin{cases} a_{11} x_1 + \ldots + a_{1n}x_n = b_1 \\ a_{22} x_2 + \dots + a_{2n} x_n = b_2 \\ \ldots \\ a_{rs} x_s + \ldots + a_{rn} x_n = b_r \\ 0 = b_{r+1} \\ \ldots \\ 0 = b_m \end{cases}\]

   И тут важный момент в последних строках: во-первых, у нас необязательно получится идеально ступенчатая матрица, и некоторые неизвестные могут сократиться процессе, а, во-вторых, может быть просто так, что $m > n$, так что в конце будут вот эти уравнения вида $0 = b_i$.

И, очевидно, что, если система в ступенчатом виде имеет уравнения вида $0 = b_i, b_i \not= 0$, то такая система несовместна. Будем называть неизвестные $x_1, x_2, \ldots, x_s$, с которых начинаются уравнения в системе, главными, а остальные будем называть свободными (если такие вообще есть). И, если подставить вместо всех свободных неизвестных какие-то значения, то становится видео, что $a_{rs} x_s + c = b_r$ имеет единственное решение, и дальше уже можно подниматься вверх по лестнице.

Таким образом, система совместна, если в её ступенчатом виде нет уравнений вида $0 = b_i, b_i \not= 0$ и совместная система является определённой, если в её ступенчатом виде $r = n$ (ну, потому что иначе есть свободные неизвестные, которые могут принять любые значения).

Некоторые очевидные следствия из всего этого:

• линейная система с $m = n$ является совместной и определённой тогда и только тогда, когда в ступенчатом виде все коэффициенты $a_{11}, a_{22}, \ldots, a_{nn} \not = 0$. (Иначе она может быть либо несовместной, если, скажем, в последнем уравнении $a_{nn} = 0$ и $b_{nn} \not = 0$, либо совместной неопределённой, если, например, в последнем уравнении $a_{nn} = 0$ и $b_{nn} = 0$.)
• условие с ненулевыми коэффициентами не зависит от свободных членов, так что можно отбросить их, и в случае $m = n$ рассматривать ассоциированную однородную систему: линейная система с $m = n$ является совместной и определённой тогда и только тогда, когда ассоциированная однородная система имеет только нулевое решение (она всегда совместна, потому что имеет нулевое решение, так что определённость равносильна отсутствию ненулевых решений).
• Если $n > m$, то, очевидно, $r < n$, а это означает наличие свободных неизвестных, что влечёт за собой неопределённость системы.

Некоторые при кольные замечания

Такой вот метод сведения системы линейных уравнений к ступенчатому виду и постепенных последующих подстановок называется методом Гаусса. Он простой, так что его вполне можно использовать для систем с небольшим количеством уравнений в программной реализации. Однако есть и более эффективные (при достаточно большом $n$) алгоритмы, а на практике и вовсе скорее будут использоваться методы приближённого вычисления корней систем уравнений.

Сложность приведения к ступенчатому виду и вычисления всех корней. Мы будем учитывать только операции умножения и деления, потому что они дороже сложений.

Некоторые прикольные формулы, которые использовались, и их вывод:

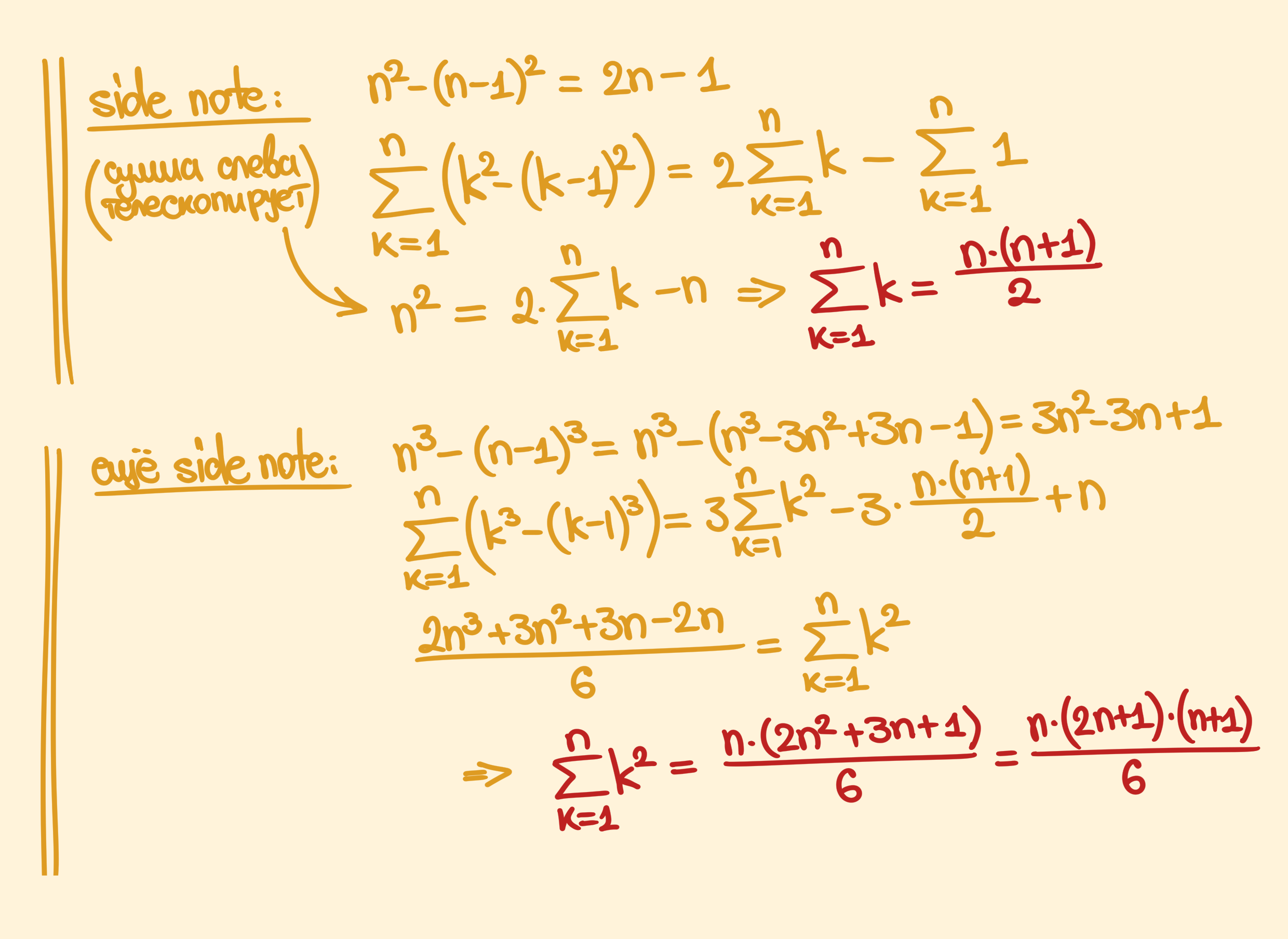
Определители небольших порядков

Короче, опять для начала рассмотрим простые системы уравнений. Для матрицы 2 x 2 будем называть определителем матрицы значение:

\[\det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right) := a_{11} a_{22} - a_{21} a_{12}\]

Попробуем избавиться от $x_2$ в этой системе уравнений: домножим первое на $-a_{22}$, второе — на $-a_{12}$, сложим их, и так можно будет вывести $x_1$.

\[\begin{cases} a_{11} x_1 + a_{12} x_2 = b_1 \\ a_{21} x_1 + a_{22} x_2 = b_1 \end{cases}\] \[\det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right) x_1 = \det\left(\begin{matrix} b_1 & a_{12} \\ b_2 & a_{22} \end{matrix}\right)\]

То есть выходит, что система из двух уравнений является определённой, если её определитель не равен нулю. А, если определитель равен нулю, то у неё либо будет бесконечное количество решений, либо ни одного. Но, если исходить из того, что определитель не равен нулю, то для корней получаются вот такие формулы:

\[x_1 = \det\left(\begin{matrix} b_1 & a_{12} \\ b_2 & a_{22} \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right),\\ x_2 = \det\left(\begin{matrix} a_{11} & b_1 \\ a_{21} & b_2 \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right)\]

Аналогично можно определить определитель матрицы третьего порядка и вывести аналогичные формулы (там в числителе вот тот столбик меняет своё положение):

\[x_1 = \det\left(\begin{matrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{matrix}\right),\\ x_2 = \det\left(\begin{matrix} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \\ \end{matrix}\right) / \det(A), \\ x_3 = \det\left(\begin{matrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \\ \end{matrix}\right) / \det(A)\]

Но мне лень расписывать, там всё очевидно.