Systems Of Linear Equations 1

The geometry of linear equations

ссылка — там вообще ничего интересного

Система линейных уравнений: $\begin{cases} a_1 x + b_1 y = c_1 \\ a_2 x + b_2 y = c_1\end{cases}$

Её можно проинтерпретировать двумя способами:

row picture
\[\left(\begin{matrix} a_1 & b_1\\ a_2 & b_2 \end{matrix}\right) \cdot \left(\begin{matrix} x \\ y \end{matrix}\right) = \left(\begin{matrix} c_1 \\ c_2 \end{matrix}\right)\] \[Ax = b\]
Эту систему уравнений можно также представить как пересечение двух прямых. В случае с тремя линейными уравнениями мы имели бы дело с тремя плоскостями, и дальше уже всё становится совсем плохо. Короче, это не очень наглядный вариант.

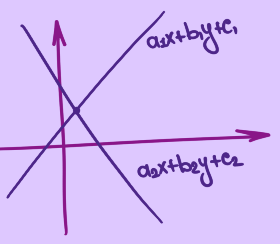
$image-20200323011154049$
column picture
\[x \cdot \left(\begin{matrix} a_1 \\ a_2 \end{matrix}\right) + y \cdot \left(\begin{matrix} b_1 \\ b_2 \end{matrix}\right) = \left(\begin{matrix} c_1 \\ c_2 \end{matrix}\right)\]
В этом случае система представляется как линейная комбинация векторов, которая равна какому-то другому вектору. То есть решение сводится к тому, что нужно определить, сколько нужно взять от первого вектора и сколько от второго, чтобы в сумме получился $\left(\begin{matrix}c1 \ c2\end{matrix}\right)$.

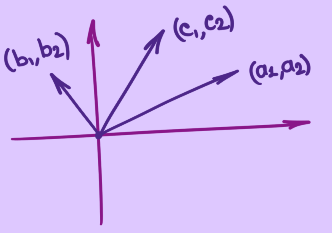
$image-20200323012117559$

Один из вопросов, который ставится в линейной алгебре: Можно ли решить уравнение $Ax = b$ для любого $b$? Его же можно поставить другим образом: Заполняют ли всё пространство линейные комбинации двух данных векторов? Очевидно, что ответ на этот вопрос не всегда положительный: например, для случая с тремя уравнениями, если все три вектора лежат в одной плоскости.

По аналогии с row/column picture произведение матрицы на вектор можно представлять как два dot-product’а, а можно, как линейную комбинацию двух векторов:

\[\left(\begin{matrix} a_1 & b_1\\ a_2 & b_2 \end{matrix}\right) \cdot \left(\begin{matrix} x \\ y \end{matrix}\right) = \left(\begin{matrix} a_1 \\ a_2 \end{matrix}\right) \cdot x + \left(\begin{matrix} b_1 \\ b_2 \end{matrix}\right) \cdot y\]

Системы линейных уравнений (2–3 порядков)

1.1–1.4 в первом томе кострикина

Терминология

Общий вид системы линейных алгебраических уравнений:

\[\begin{cases} a_{11} x_1 + a_{12} x_2 + \ldots + a_{1n} x_n = b_1 \\ a_{21} x_1 + a_{22} x_2 + \ldots + a_{2n} x_n = b_2 \\ \ldots \\ a_{m1} x_1 + a_{m2} x_2 + \ldots + a_{mn} x_n = b_m \\ \end{cases} (1)\]

Такая система называется однородной, если все свободные члены (все $b_i$) равны нулю. Система, аналогичная системе $(1)$, но с обнулёнными свободными членами называется приведённой системой.

Система, не имеющая ни одного решения, называется несовместной, иначе — называется совместной. Если решение единственное, то система называется определённой, если же решений несколько или ни одного, то система называется неопределённой.

Эквивалентность линейных систем

Элементарное преобразование типа (I) — когда меняем в системе два уравнения местами
Элементарное преобразование типа (II) — это, когда берём в системе какое-то уравнение, домножаем его на какое-то число, и прибавляем всё это к какому-то другому уравнению, так что получается что-то вроде:
\[(a_{i1} + c a_{k1}) x_1 + \ldots + (a_{in} + c a_{kn}) x_n = b_i + c b_k\]

Будем говорить, что две линейные системы называются эквивалентными, если обе они либо несовместны, либо совместны и их решения совпадают.

Теорема 1: Две линейные системы эквивалентны, если одна получается из другой путём применения конечной последовательности элементарных преобразований.

Доказательство: Если доказать, что после применения любого из элементарных преобразований получается эквивалентная система, то из этого будет следовать, что после любой последовательности элементарных преобразований получится эквивалентная система. А ещё можно доказывать теорему только в одну сторону, потому что элементарные преобразования обратимы: нужно только доказать, что любое решение первой системы является также решением второй (а это очевидно, мне лень писать).

Приведение к ступенчатому виду

Путём элементарных преобразований можно привести систему уравнений к более простому виду:

Найдём уравнение, у которого бы первый коэффициент $a_{i1}$ был ненулевым (если такого нет, то переменная $x_1$ может принимать любое значение, можно забить на неё и перейти к следующей).
Ставим это уравнение первым в системе, и прибавляем его ко всем остальным, домножив на такой коэффициент, чтобы во всех остальных уравнениях первый коэффициент обнулился.
Повторяем всё то же самое для оставшихся уравнений, пока не получим уравнение вида:
\[\begin{cases} a_{11} x_1 + \ldots + a_{1n}x_n = b_1 \\ a_{22} x_2 + \dots + a_{2n} x_n = b_2 \\ \ldots \\ a_{rs} x_s + \ldots + a_{rn} x_n = b_r \\ 0 = b_{r+1} \\ \ldots \\ 0 = b_m \end{cases}\]
И тут важный момент в последних строках: во-первых, у нас необязательно получится идеально ступенчатая матрица, и некоторые неизвестные могут сократиться процессе, а, во-вторых, может быть просто так, что $m > n$, так что в конце будут вот эти уравнения вида $0 = b_i$.

И, очевидно, что, если система в ступенчатом виде имеет уравнения вида $0 = b_i, b_i \not= 0$, то такая система несовместна. Будем называть неизвестные $x_1, x_2, \ldots, x_s$, с которых начинаются уравнения в системе, главными, а остальные будем называть свободными (если такие вообще есть). И, если подставить вместо всех свободных неизвестных какие-то значения, то становится видео, что $a_{rs} x_s + c = b_r$ имеет единственное решение, и дальше уже можно подниматься вверх по лестнице.

Таким образом, система совместна, если в её ступенчатом виде нет уравнений вида $0 = b_i, b_i \not= 0$ и совместная система является определённой, если в её ступенчатом виде $r = n$ (ну, потому что иначе есть свободные неизвестные, которые могут принять любые значения).

Некоторые очевидные следствия из всего этого:

линейная система с $m = n$ является совместной и определённой тогда и только тогда, когда в ступенчатом виде все коэффициенты $a_{11}, a_{22}, \ldots, a_{nn} \not = 0$. (Иначе она может быть либо несовместной, если, скажем, в последнем уравнении $a_{nn} = 0$ и $b_{nn} \not = 0$, либо совместной неопределённой, если, например, в последнем уравнении $a_{nn} = 0$ и $b_{nn} = 0$.)
условие с ненулевыми коэффициентами не зависит от свободных членов, так что можно отбросить их, и в случае $m = n$ рассматривать ассоциированную однородную систему: линейная система с $m = n$ является совместной и определённой тогда и только тогда, когда ассоциированная однородная система имеет только нулевое решение (она всегда совместна, потому что имеет нулевое решение, так что определённость равносильна отсутствию ненулевых решений).
Если $n > m$, то, очевидно, $r < n$, а это означает наличие свободных неизвестных, что влечёт за собой неопределённость системы.

Некоторые при кольные замечания

Такой вот метод сведения системы линейных уравнений к ступенчатому виду и постепенных последующих подстановок называется методом Гаусса. Он простой, так что его вполне можно использовать для систем с небольшим количеством уравнений в программной реализации. Однако есть и более эффективные (при достаточно большом $n$) алгоритмы, а на практике и вовсе скорее будут использоваться методы приближённого вычисления корней систем уравнений.

Сложность приведения к ступенчатому виду и вычисления всех корней. Мы будем учитывать только операции умножения и деления, потому что они дороже сложений.

$image-20200328233059934$

Некоторые прикольные формулы, которые использовались, и их вывод:

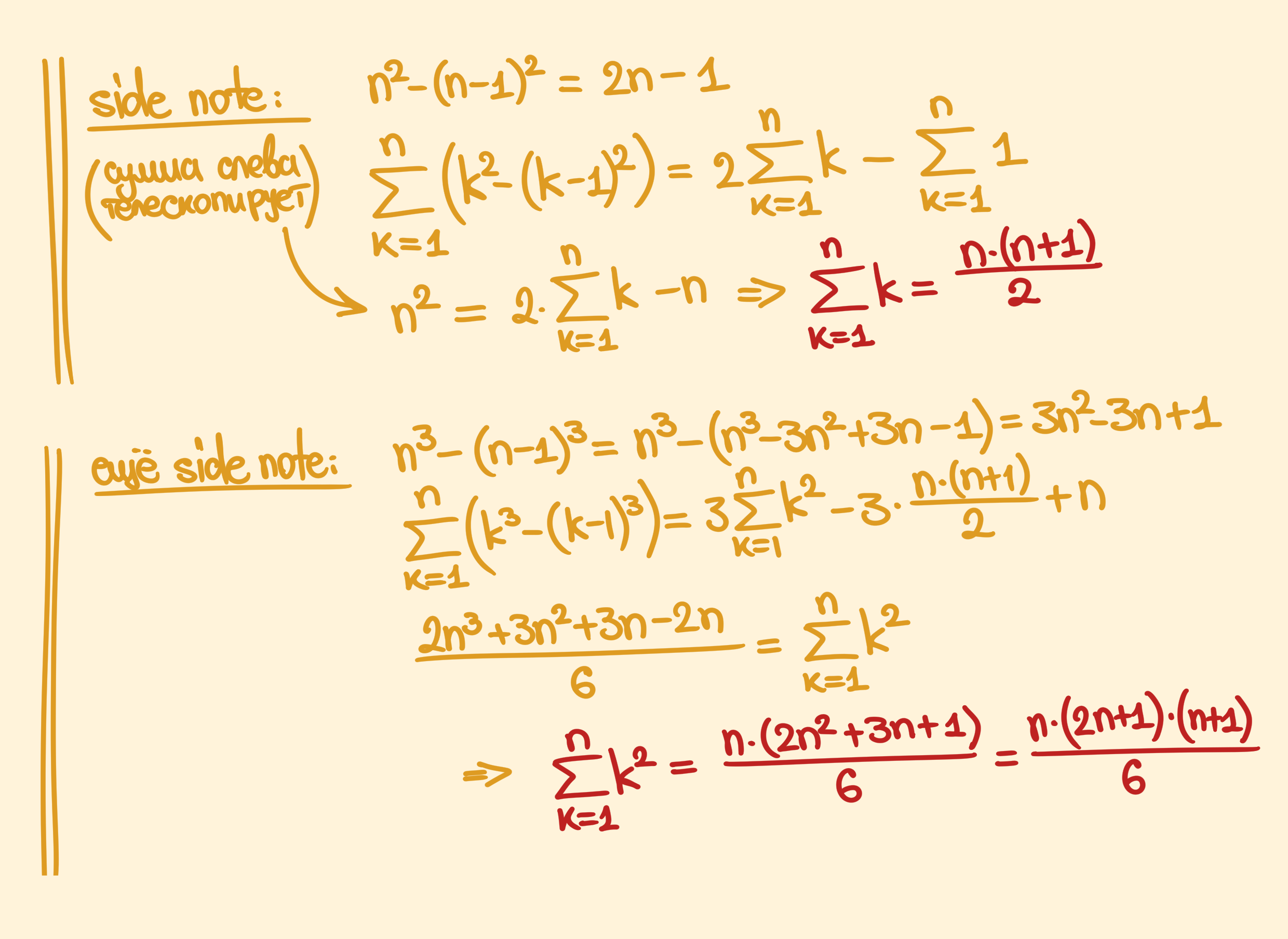
$image-20200328233334267$

Определители небольших порядков

Короче, опять для начала рассмотрим простые системы уравнений. Для матрицы 2 x 2 будем называть определителем матрицы значение:

\[\det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right) := a_{11} a_{22} - a_{21} a_{12}\]

Попробуем избавиться от $x_2$ в этой системе уравнений: домножим первое на $-a_{22}$, второе — на $-a_{12}$, сложим их, и так можно будет вывести $x_1$.

\[\begin{cases} a_{11} x_1 + a_{12} x_2 = b_1 \\ a_{21} x_1 + a_{22} x_2 = b_1 \end{cases}\] \[\det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right) x_1 = \det\left(\begin{matrix} b_1 & a_{12} \\ b_2 & a_{22} \end{matrix}\right)\]

То есть выходит, что система из двух уравнений является определённой, если её определитель не равен нулю. А, если определитель равен нулю, то у неё либо будет бесконечное количество решений, либо ни одного. Но, если исходить из того, что определитель не равен нулю, то для корней получаются вот такие формулы:

\[x_1 = \det\left(\begin{matrix} b_1 & a_{12} \\ b_2 & a_{22} \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right),\\ x_2 = \det\left(\begin{matrix} a_{11} & b_1 \\ a_{21} & b_2 \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix}\right)\]

Аналогично можно определить определитель матрицы третьего порядка и вывести аналогичные формулы (там в числителе вот тот столбик меняет своё положение):

\[x_1 = \det\left(\begin{matrix} b_1 & a_{12} & a_{13} \\ b_2 & a_{22} & a_{23} \\ b_3 & a_{32} & a_{33} \end{matrix}\right) / \det\left(\begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{matrix}\right),\\ x_2 = \det\left(\begin{matrix} a_{11} & b_1 & a_{13} \\ a_{21} & b_2 & a_{23} \\ a_{31} & b_3 & a_{33} \\ \end{matrix}\right) / \det(A), \\ x_3 = \det\left(\begin{matrix} a_{11} & a_{12} & b_1 \\ a_{21} & a_{22} & b_2 \\ a_{31} & a_{32} & b_3 \\ \end{matrix}\right) / \det(A)\]

Но мне лень расписывать, там всё очевидно.

Оглавление