Оглавление

• Линейные отображения. Действия с матрицами (продолжение)
  • Ранг произведения матриц
  • Квадратные матрицы
  • Обратные матрицы
  • Следствия из теоремы про существование обратной матрицы

Линейные отображения. Действия с матрицами (продолжение)

---

продолжение 2.3 в первом томе кострикина

ранг произведения матриц (неравенство), квадратные матрицы, единичные/скалярные матрицы и их свойства, доказательство того, что только скалярные матрицы являются перестановочными с любыми другими квадратными матрицами, обратные матрицы, (не)вырожденные матрицы, теорема об обратимости матрицы

следствия из теоремы про обратимость матриц: неизменность ранга при домножении на невырожденную, обратимость из существования левой/правой обратной матрицы, матрица обратная произведению n невырожденных матриц

---

Ранг произведения матриц

Теорема. Пусть $A$ — произвольная матрица размера $m \times s$, $B$ — матрица размера $s \times n$. Тогда для них справедливо неравенство $\text{rank} AB \leq \min{\text{rank} A,\text{rank} B}$. То есть по сути это означает, что при перемножении двух матриц ранг не может увеличиться.

Доказательство. По определению произведения матриц:

\[C_{(i)} = A_{(i)}B \text{ - равенство для строк результирующей матрицы.}\\ С^{(j)} = AB^{(j)} \text{ - равенство для столбцов результирующей матрицы.}\]

Возьмём в качестве ранга матрицы $A$ её строчный ранг: $r_1 = \text{rank} A = \dim\left<A_{(1)},A_{(2)}, \dots, A_{(m)}\right>$. Не умаляя общности также примем строки $A_{(1)}, \dots, A_{(r_1)}$ за базисные, потому что перестановка строк — это элементарное преобразование, которое не изменит ранг ни матрицы $A$, ни $C$,

Из этого следует, что можно выразить все остальные строки матрицы $A$ через линейную комбинацию базисных строк, а значит, соответствующие строки матрицы $C$ тоже выражаются через первые свои $r_1$ строк:

\[C_{(k)} = A_{(k)} B = (\sum_{i = 1}^{r_1} \lambda_{ki} A_{(i)}) B = \sum_{i = 1}^{r_1} \lambda_{ki} (A_{(i)}B) = \sum_{i = 1}^{r_1} \lambda_{ki} C_{(i)}\]

Из чего следует, что набор из первых $r_1$ строк матрицы $C$ как минимум является порождающим, так что $\text{rank} C \leq r_1 = \text{rank} A$. Аналогичным образом выводится, что $\text{rank} C \leq \text{rank} B\,\,\,\square$

---

Квадратные матрицы

Множество всех квадратных матриц порядка $n$ с вещественными коэффициентами обозначается как $M_n(\mathbb{R})$ или $M_n$. Можно также рассматривать это множество как векторное пространство (потому что выполняются все аксиомы (ассоциативность и дистрибутивность уже выводились ранее) и все операции замкнуты). Также говорят, что множество $M_n$ образует матричное (ассоциативное) кольцо, а с учётом того, что также выполняются свойства $\lambda AB = (\lambda A) B = A (\lambda B)$, множество $M_n$ также называется алгеброй матриц над $\mathbb{R}$. (Я не помню определение кольца, и даже не знаю определения алгебры, но, я так понимаю, всё это будет объяснено позже.)

Также, говоря о квадратных матрицах, надо обратить внимание на единичные матрицы, которые определяются вот так: $E_n := (\delta_{kj})$, где $\delta_{kj}$ — это символ Кронекера, который определяется вот так:

\[\delta_{kj} = \begin{cases} 1, \text{ если } k = j \\ 0, \text{ если } k \not = j \end{cases}\]

Свойства единичных и скалярных матриц. Очевидно, что для единичных матриц верно, что $\text{rank} E_n = n$. А ещё верно то, что $EA = A = AE$ для любой матрицы $A \in M_n$. И вот так в общем случае: $\text{diag}_n(\lambda) A = \lambda A = A\, \text{diag}_n(\lambda)$, где $\text{diag}_n(\lambda)$ определяется как $\text{diag}_n(\lambda) = \lambda E$ — это скалярная матрица.

Теорема. Если $A \in M_n$ — такая матрица, что она перестановочна со всеми матрицами из $M_n$ (то есть $AB = BA,\, \forall B \in M_n$), то она должна быть скалярной.

Доказательство. Определим матрицу $E_{ij}$ как матрицу, в которой элемент $(i, j)$ равняется единице, а остальные — нулевые. Если $A$ — та перестановочная матрица из определения теоремы, то для неё выполнится равенство $A E_{ij} = E_{ij}A,\,\forall i,j$. Можно расписать произведение матриц вот так:

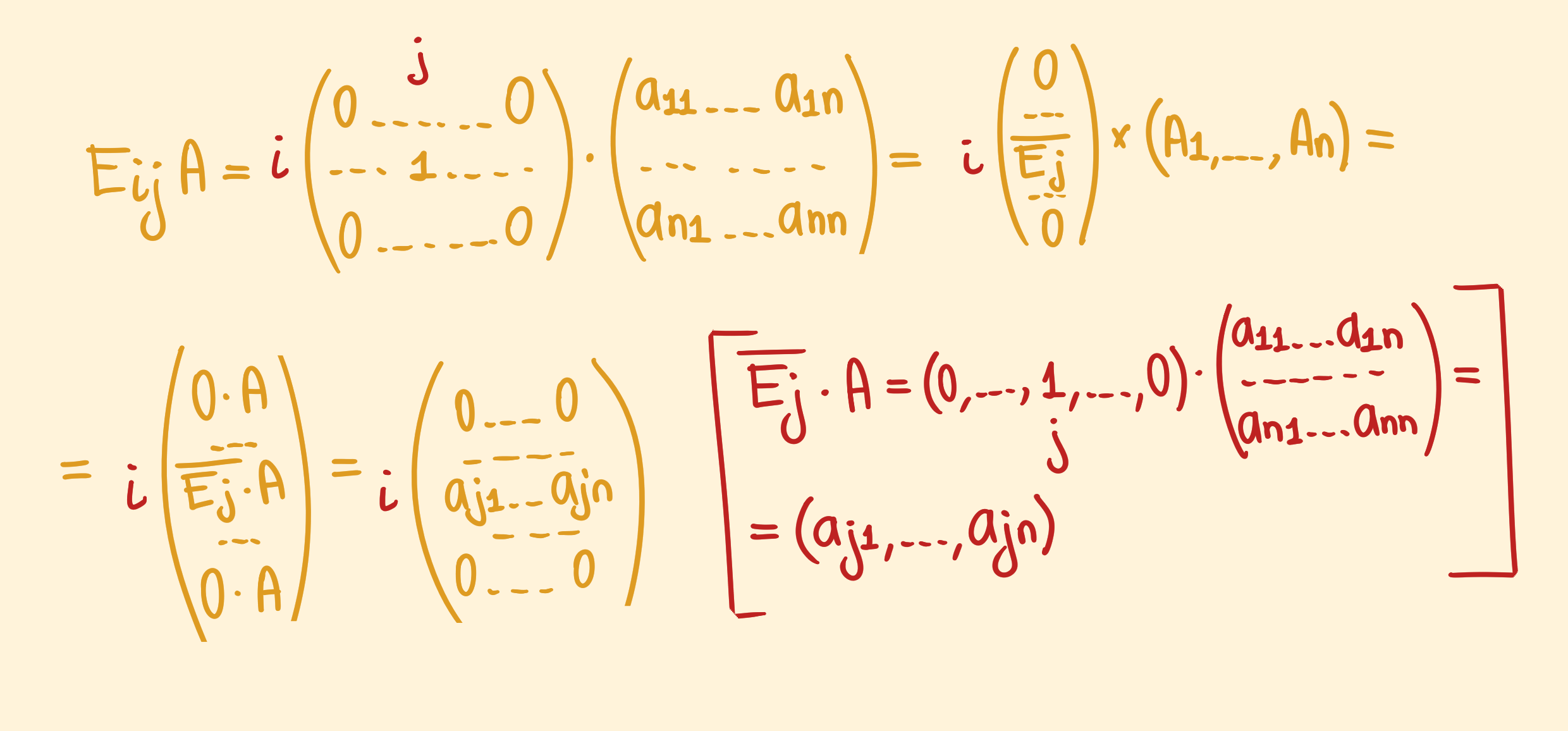
Аналогично можно расписать произведение $A E_{ij}$ (получится единственный ненулевой $j$-ый столбец). И в силу равенства:

\[\left(\begin{matrix} 0 & \dots & 0 \\ \dots & \dots & \dots \\ a_{j1} & \dots & a_{jn} \\ \dots & \dots & \dots \\ 0 & \dots & 0 \end{matrix}\right) = E_{ij}A = A E_{ij} = \left(\begin{matrix} 0 & \dots & a_{1i} & \dots & 0 \\ \dots & \dots & \dots & \dots & \dots\\ 0 & \dots & a_{ni} & \dots & 0 \end{matrix}\right)\]

Из этого следует, что $a_{jk} = 0,\, \forall k\not = j$ и $a_{jj} = a_{ii}$. Задавая разные значения $i$ и $j$ выводится, что все диагональные элементы равны, а те, что находятся не на диагонали, равны нулю. То есть $\text{diag}_n(\lambda) = A\,\,\square$

---

Обратные матрицы

Единственность обратной матрицы. Для данной квадратной матрицы $A \in M_n$ может существовать такая матрица $A’ \in M_n$, чтобы выполнялось соотношение $AA’ = E_n = A’A$. Сразу же можно вывести единственность такой матрицы при условии её существования. Если существует другая матрица $A’’$ такая, что $AA’’ = A’‘A = E$, то: $A’’ = A’’ E = A’’ (AA’) = (A’’ A) A’ = E A’ = A’$.

Такая матрица называется обратной к $A$ и обозначается как $A^{-1}$. Если для матрицы существует обратная, то она называется обратимой.

Определение. Матрица $A \in M_n(\mathbb{R})$ называется невырожденной, если $\text{rank} A = n$. Если же $\text{rank} A \lt n$, то матрица называется вырожденной.

Теорема. Матрица $A \in M_n$ является обратимой тогда и только тогда, когда она не является вырожденной.

Доказательство $(\implies)$ Предположим, что матрица является обратимой, из чего следует в частности, что $AB = E$. $n = \text{rank} E = \text{rank} AB \leq \min {\text{rank}A, \text{rank} B} \leq n$. Последнее неравенство просто следует просто из того, что $A,B \in M_n$. Из этого следует, что $\min {\text{rank}A, \text{rank} B} = n \implies \text{rank} A = n,\,\,\text{rank} B = n\,\,\square$

Доказательство $(\impliedby)$ Предположим теперь, что $\text{rank} A = n$. Из этого следует, что все столбцы матрицы $A$ линейно независимы, а значит, их линейная комбинация порождает всё пространство $\mathbb{R}^n$ и являются базисными для него. Так что можно выразить стандартный базис через этот другой базис:

\[E^{(j)} = \sum_{i = 1}^n a_{ij}' A^{(i)}\]

Координаты для стандартного базиса в терминах нового можно выписать в виде матрицы из $M_n$, причём выписать их по столбцам. Назовём эту матрицу $A’$.

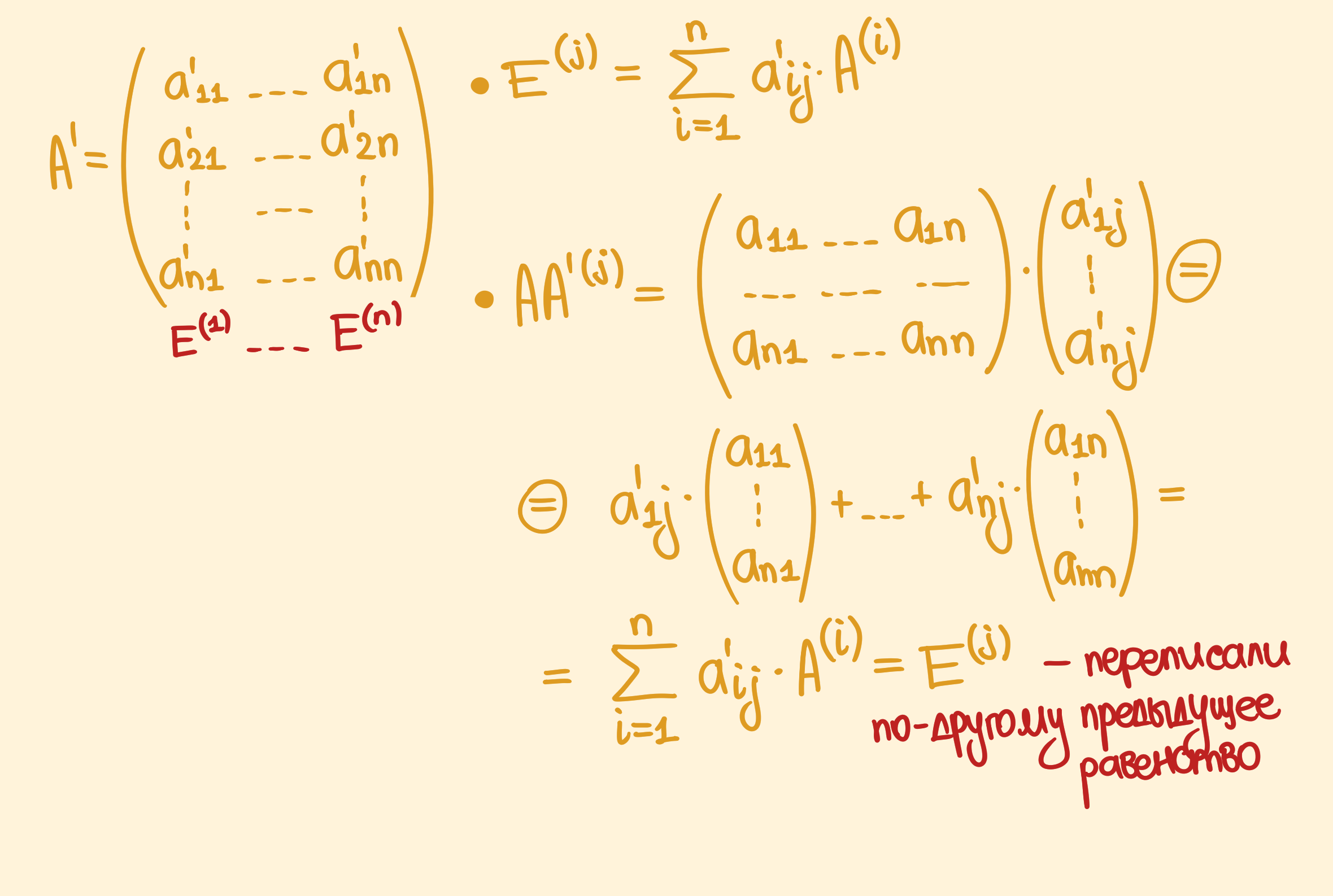
Равенство выше можно немного переписать:

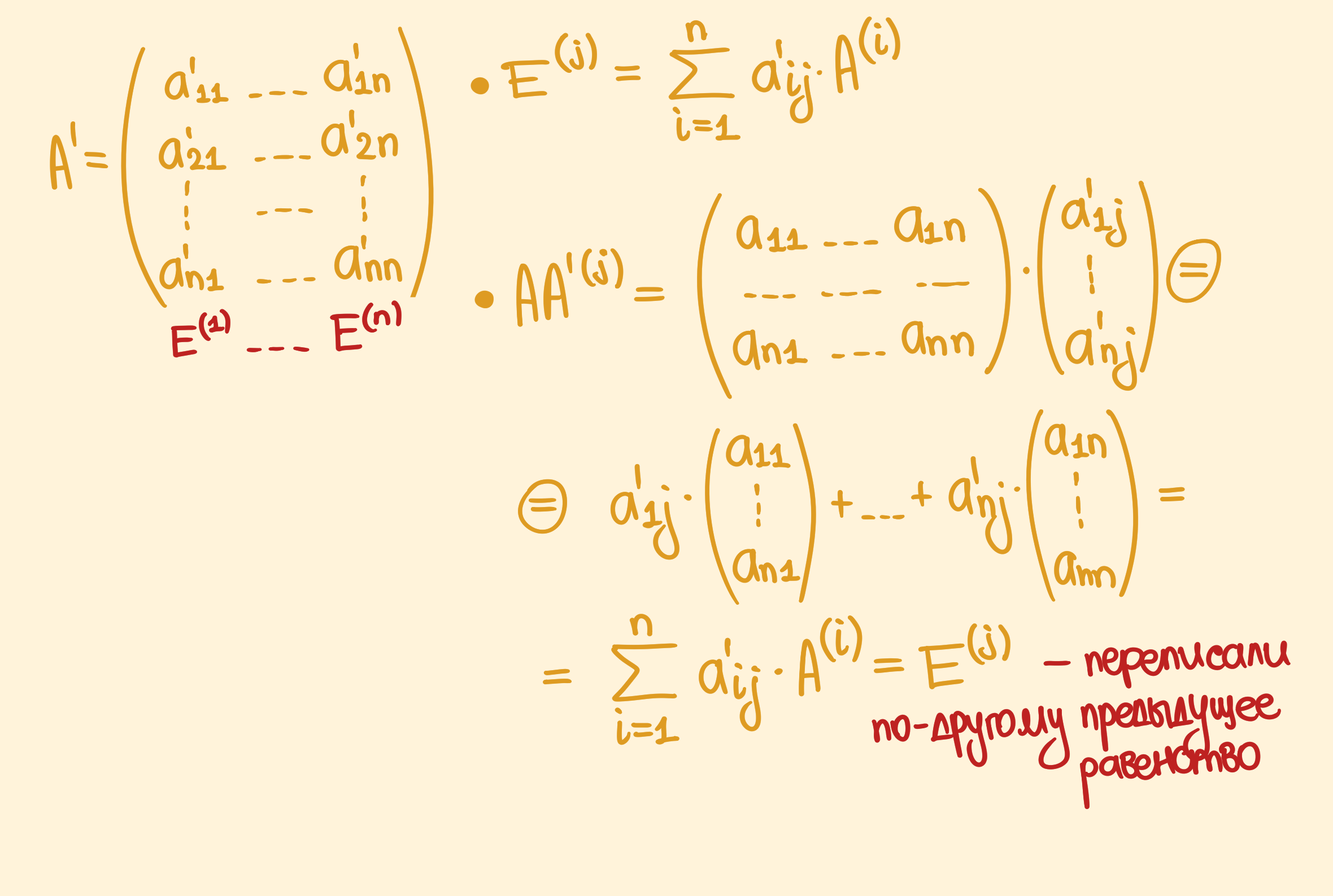
И тогда получится, что $E = (E^{(1)}, \dots, E^{(n)}) = (AA’^{(1)}, \dots, AA’^{(n)}) = AA’$. То есть нашли обратную к $A$ справа. Теперь можно проделать всё то же самое для транспонированной матрицы $A^T$. Для неё найдётся такая матрица $B$, что $A^T B = E \implies E = E^T = (A^T B)^T = B^T (A^T)^T = B^T A$. Так что нашли обратную слева $A’’ = B^T$.

Допустим, есть обратная справа: $AA’ = E$. $A’’ = A’’ E = A’’ (AA’) = (A’’ A) A’ = E A’ = A’$. То есть, если есть обратные слева и справа, то они будут обязательно равны. Так, доказали, что у невырожденной матрицы есть обратная $\square$

---

Следствия из теоремы про существование обратной матрицы

Теорема. Если $B \in M_m,\, \text{rank}B = m$ и $C \in M_n,\, \text{rank} C = n$, и $A$ — матрица $m \times n$, то:

\[\text{rank} BAC = \text{rank}A\]

Доказательство. Так как при умножении матрицы на другую матрицу её ранг не увеличивается, то:

\[\text{rank} BAC = \text{rank} (BA)C \leq \text{rank BA} = [\text{в силу невырожденности матрицы }C]\\ = \text{rank}(BA(CC^{-1})) = \text{rank}((BAC)C^{-1}) \leq \text{rank}(BAC)\]

Из этого следует, что $\text{rank}BAC = \text{rank} BA$. Аналогично:

\[\text{rank}BA \leq \text{rank} A = \text{rank}B^{-1} (BA) \leq \text{rank} BA\]

И отсюда уже следует $\text{rank}BAC = \text{rank}BA = \text{rank}A\,\,\square$

---

Теорема. Если $A,B \in M_n$ и $AB = E$ или $BA = E$, то из этого сразу следует, что $B = A^{-1}$.

Доказательство. $n = \text{rank} E = \text{rank} AB \leq \text{rank} A \leq n \implies \text{rank} A = n$. То есть невырожденность следует только лишь существования левого/правого обратного, а не обратимости в целом. А по доказанной теореме, раз есть невырожденность, то есть и обратимость $\square$

---

Теорема. Если $A,B,\dots,C,D \in M_n$ — невырожденные матрицы, то их произведение, тоже будет невырожденной матрицей (ну, это очевидно из того первого следствия про ранг матрицы, умноженной слева и справа на невырожденные матрицы $\text{rank} BAC = \text{rank}A$), и ещё имеет место вот такое равенство:

\[(AB\dots CD)^{-1} = D^{-1} C^{-1}\dots B^{-1} A^{-1}\]

Доказательство. Можно проверить, просто умножив вручную и воспользовавшись предыдущей теоремой, чтобы не надо было проверять обратимость и слева, и справа:

\[(AB\dots CD) (D^{-1} C^{-1} \dots B^{-1} A^{-1}) = AB\dots C(DD^{-1})C^{-1}\dots B^{-1} A^{-1} = \dots = E\,\,\square\]

Оглавление

• Ранг матрицы
  • Опять решения систем линейных уравнений
  • Ранг матрицы
• Линейные отображения. Действия с матрицами
  • Матрицы и отображения
  • Произведение матриц
  • Транспонирование матриц

Ранг матрицы

---

2.2 в первом томе кострикина

определение решения системы линейных уравнений в терминах вот этих всех линейных оболочек, ранг матрицы по столбцам и по строкам, инвариантность рангов относительно элементарных преобразований, равенство рангов по строкам и столбцам, теорема кронекера-капелли

---

Опять решения систем линейных уравнений

Альтернативное определение решения системы уравнений. Пусть мы находимся в векторном пространстве $\mathbb{R}^m$ из столбцов $A^{(j)} = [a_{1j}, a_{2j},\dots, a_{mj}]$. (Соглашения об обозначениях. Столбцы обозначаем с индексом наверху, но, чтобы это не конфликтовало со степенью, засовываем индекс в скобки. Сами столбцы выписываем горизонтально, но в квадратных скобках.) Пусть у нас есть ещё один вектор из $\mathbb{R}^m$ $B = [b_1, b_2, \dots, b_m]$. Нам нужно определить, принадлежит ли вектор $B$ линейной оболочке $V = \left<A_1, \dots, A_n\right>$, и через какие коэффициенты выражается $B$ через эти векторы. По сути этот вопрос эквивалентен вопросу решения соответствующей системы уравнений:

\[x_1 \left(\begin{matrix}a_{11}\\a_{21}\\ \vdots \\ a_{m1}\end{matrix} \right) + x_2 \left(\begin{matrix}a_{12}\\a_{22}\\ \vdots \\ a_{m2}\end{matrix} \right) + \dots + x_n \left(\begin{matrix}a_{1n}\\a_{2n}\\ \vdots \\ a_{mn}\end{matrix} \right) = \left(\begin{matrix}b_{1}\\b_{2}\\ \vdots \\ b_{m}\end{matrix} \right)\\\] \[(A \mid B) = \left(\begin{array}{cccc|c} a_{11} & a_{12} & \dots & a_{1n} & b_1 \\ a_{21} & a_{22} & \dots & a_{2n} & b_2 \\ \dots & \dots & \dots & \dots & \dots\\ a_{m1} & a_{m2} & \dots & a_{mn} & b_m \\ \end{array}\right)\]

---

Ранг матрицы

Назовём пространством столбцов прямоугольной $m \times n$ матрицы $A$ линейную оболочку $V_v = \left<A^{(1)}, \dots, A^{(n)}\right>$ (“v” от vertical). Аналогичным образом вводится пространство строк матрицы $A$: $V_h$ (“h” от horizontal). Размерность $r_v(A) = \dim V_v$ будем называть рангом по столбцам матрицы, $r_h(A) = \dim V_h$ — ранг по строкам матрицы.

\[r_v(A) = \text{rank}\{A^{(1)},A^{(2)}, \dots,A^{(n)}\} \\ r_h(A) = \text{rank}\{A_{(1)},A_{(2)}, \dots,A_{(m)}\}\]

По аналогии с тем, как мы определили элементарные преобразования для системы линейных уравнений , можно определить их и для матрицы (первый тип — перестановка строк, второй тип — домножение строки на скаляр и прибавление её к другой строке).

Лемма. Если матрица $A’$ получена из матрицы $A$ путём конечной последовательности элементарных преобразований над строками, то имеют место равенства:

\[r_v(A') = r_v(A)\\ r_h(A') = r_H(A)\]

Доказательство. Для доказательства достаточно доказать, что равенства сохраняется после применения одного произвольного элементарного преобразования. Рассмотрим для начала ранг по строкам матрицы. Если мы поменяем какие-то две строки местами, то, очевидно, линейная пространство строк вообще никак не поменяется, потому что какая разница, в каком порядке они расположены. Теперь элементарное преобразование второго типа:

\[A'_{(s)} = A_{(s)} + \lambda A_{(t)} \text{ - элементарное преобразование}\\ \left<A_{(1)}, \dots, A_{(s)} + \lambda A_{(t)}, \dots,A_{(t)},\dots,A_{(m)} \right> = \left<A_{(1)}, \dots, A_{(s)}, \dots,A_{(t)},\dots,A_{(m)} \right>\]

Теперь рассмотрим ранг по столбцам матрицы. Для этого для начала докажем, что:

\[\sum_{j = 1}^l \lambda_j A^{(j)} = 0 \iff \sum_{j = 1}^l \lambda_j A'^{(j)}\]

Это очевидно из того, что мы уже доказали, что решения систем уравнений, полученных друг из друга элементарными преобразованиями, совпадают, причём с точностью до порядка значений неизвестных в решениях системы. Из этого следует, что если мы возьмём $l$ любых линейно независимых столбцов в матрице до преобразования, то после преобразования они останутся линейно независимыми. В том числе, если взять базис пространства столбцов до преобразования, то он останется базисом и после преобразования, что доказывает, что ранг не изменится после преобразований $\square$

(Не изменится, потому что, если бы он увеличился, то можно было найти большую линейно независимую порождающую систему до преобразования. А уменьшиться он не может, потому что он как минимум остаётся таким же.)

---

Теорема. Для любой прямоугольной $m \times n$ матрицы $A$ справедливо равенство $r_h(A) = r_v(A)$. Это число называется рангом матрицы $A$ и обозначается как $\text{rank}(A)$.

Доказательство. Уже разобрались с тем, что любую матрицу (систему линейных уравнений) можно привести к ступенчатому виду:

По предыдущей лемме после преобразования ни горизонтальный ранг матрицы, ни вертикальный, не изменятся. Столбцы матрицы $1,k,l,\dots,s$ будем называть базисными столбцами. (То есть выбрали все столбцы, в которых разное количество ненулевых значений.) Такой набор из $r$ столбцов (я на некоторое время завис на этом, потому что не сразу увидел, что базисных столбцов там действительно $r$ штук) будет линейно независимым:

\[\lambda_1 A^{(1)} + \lambda_k A^{(k)} + \lambda_l A^{(l)} + \dots + \lambda_s A^{(s)} = 0 \\ A^{(1)} = [a_{11},0,\dots,0],\,\,A^{k} = [a_{1k},a_{2k},0,\dots,0],\dots,A^{(s)} = [a_{1s},\dots,a_{rs}] \\ \implies \lambda_s a_{rs} = 0,\,\, \dots,\,\,\lambda_l a_{3l} = 0,\,\,\lambda_l a_{3l} = 0,\,\,\lambda_k a_{2k} = 0,\,\,\lambda_1 a_{11} = 0\]

Из этого следует, что $r_v(A) \geq r$. Однако $\left<A^{(1)},A^{(k)},\dots,A^{(s)}\right> = \mathbb{R}^r$ (ну, не совсем так, но, если отождествить $(a_1, \dots,a_r) = (a_1, \dots, a_r, 0, \dots, 0)$, то оно будет так. Ну, из этого следует, что любой линейно независимый набор в линейной оболочке этих базисных столбцов имеет $\leq r$ элементов. Так что $r_v(A) = r$.

Аналогично получается, что первые $r$ строк в матрице $A$ линейно независимы, из чего будет следовать, что $r_h(A) \geq r$. И при этом пространство строк таблицы порождается только вот этими $r$ ненулевыми первыми строками. То есть это базис по определению, а значит, $r_h(A) = r$.

Так что получается: $r_h(A) = r = r_v(A)$. И это равенство для преобразованной матрицы, но по предыдущей лемме элементарные преобразования не меняют ранг матрицы по строкам/столбцам, так что равенство рангов будет верно и для матрицы до преобразования $\square$

---

Таким образом, вывели то, что число главных неизвестных равно рангу матрицы.

Теорема Кронекера-Капелли. Система линейных уравнений совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы совпадает с рангом расширенной матрицы системы.

Доказательство ($\implies$). Если расписать систему линейных уравнений по столбцам, то совместность системы трактуется как вопрос о том, можно ли представить вектор $B$ как линейную комбинацию векторов-столбцов. Если такое представление возможно, то: $B \in \left<A^{(1)}, \dots, A^{(n)}\right>$ и $\text{rank}(A^{(1)}, \dots, A^{(n)}) = \text{rank}(A^{(1)},\dots,A^{(n)},B)$ (потому что добавление вектора, который линейно выражается через остальные не меняет базиса) $\square$

Доказательство ($\impliedby$). Теперь предположим, что ранги матриц $(A \mid B)$ и $A$ совпадают. Допустим, что ${A^{(j_1)}, \dots, A^{(j_r)}}$ — это какой-то базисный набор столбцов матрицы $A$. Если добавить к ней любой один вектор (в том числе $B$), то набор станет линейно зависимым, так что можно будет выразить $B$ через выбранные базисные векторы, что эквивалентно разрешимости системы $\square$

Линейные отображения. Действия с матрицами

---

2.3 в первом томе кострикина

определение линейного отображения, матрица линейного отображения, линейная комбинация линейных отображений (то, что это линейное отображение, и формула для матрицы), композиция линейных отображений, произведение матриц, свойства произведения матриц

---

Матрицы и отображения

Определение линейного отображения. Пусть $\mathbb{R}^n$ и $\mathbb{R}^m$ — векторные пространства столбцов, $A = (a_{ij})$ — матрица размера $m \times n$. Определим отображение $\phi_A: \mathbb{R}^n \rightarrow \mathbb{R}^m$, которое отображает любой вектор $X = [x_1, x_2, \dots, x_n] \in \mathbb{R}^n$ следующим образом:

\[\phi_A(X) = x_1 A^{(1)} + x_2 A^{(2)} + \dots + x_n A^{(n)}\]

Ну, или ещё можно вот так определить (вектор $X$ отображается в вектор $Y$):

\[\left(\begin{matrix} y_1 \\ \vdots \\ y_m \end{matrix}\right) = \left( \begin{matrix} a_{11} & \dots & a_{1n} \\ \dots & \dots & \dots \\ a_{m1} & \dots & a_{mn} \end{matrix}\right) \left(\begin{matrix} x_1 \\ \vdots \\ x_n \end{matrix}\right) = \left(\begin{matrix} a_{11} x_1 + \dots + a_{1n}x_n \\ \vdots \\ a_{m1} x_1 + \dots + a_{mn}x_n \end{matrix}\right)\]

Можно вывести вот такие свойства отображения $\phi_A$:

• $\phi_A(X’ + X’’) = \sum_{i = 1}^n (x_i’ + x_i’’) A^{(i)} = \sum_{i = 1}^n x_i’’ A^{(i)} + \sum_{i = 1}^n x_i’’ A^{(i)} = \phi_A(X’) + \phi(X’’)$ — аддитивность.

• $\phi_A(\lambda X) = \sum_{i = 1}^n (\lambda x_i) A^{(i)} = \lambda \phi_A(X)$ — не знаю, как такое называется.

Теперь попробуем подойти с другой стороны: допустим, у нас есть произвольное отображение $\phi: \mathbb{R}^n \rightarrow \mathbb{R}^m$, которое обладает вышеуказанными свойствами. Из этих свойств следует вот это равенство (раскладываем аргумент $X$ по базисным векторам):

\[\phi(X) = \phi(\sum_{i = 1}^n x_i E^{(i)}) = \sum_{i + 1}^n x_i \phi(E^{(i)})\]

То есть отображение с такими свойствами полностью определяется своими значениями на базисных векторах. Если взять в качестве этих значений столбцы матрицы $A$: $\phi(E^{(i)}) := A^{(i)}$, то мы получим как раз определение отображения $\phi_A$.

Отображение $\phi = \phi_A : \mathbb{R}^n \rightarrow \mathbb{R}^m$, которое обладает свойствами $\phi(X_1 + X_2) = \phi(X_1) + \phi(X_2)$ и $\phi(\lambda X) = \lambda \phi(X)$, называется линейным отображением из $\mathbb{R}^n$ в $\mathbb{R}^m$. Если $n=m$, то его ещё называют линейным преобразованием. Матрица $A$ называется матрицей линейного отображения. (Если матрицы линейных отображений совпадают, то совпадают и соответствующие им линейные отображения, и наоборот, то есть есть взаимно однозначное соответствие между матрицами $m \times n$ и линейными отображениями из $\mathbb{R}^n$ в $\mathbb{R}^m$.)

В частности можно говорить о линейных функциях от $n$ переменных, которые определяются как линейные отображения из $\mathbb{R}^n$ в $\mathbb{R}$ и задаются $n$ скалярами $a_1,\dots,a_n$:

\[\phi(X) = \phi(x_1,\dots,x_n) = a_1 x_1 + \dots + a_n x_n\]

Линейная комбинация линейных отображений является линейным отображением с матрицей, равной линейной комбинации матриц исходных отображений. (Жесть ужасно сложно звучит, но на деле это выглядит довольно очевидной штукой.) То, что это линейное отображение, проверяется просто по определению этих двух свойств. Пусть $C$ — матрица отображения $\phi$, тогда:

\[C^{(i)} = \phi(E^{(i)}) = \alpha \phi_A(E^{(i)}) + \beta \phi_B(E^{(i)}) = \alpha A^{(i)} + \beta B^{(i)} \\ \implies C = \alpha A + \beta B\]

---

Произведение матриц

По аналогии с тем, как линейная комбинация линейных отображений является линейным отображением, композиция линейных отображений — это тоже линейное отображение. Это легко проверить. И тут интереснее то, какая получается матрица у композиции отображений:

Матрицу композиции отображений будем называть произведением матриц $A$ и $B$. При этом смысл произведения матриц $AB$ имеет смысл только, когда число столбцов первой матрицы равно числу строк во второй матрице (это как раз связано с тем, как мы определили произведение матриц через композицию отображений). А число строк результирующей матрицы равно числу строк в первой матрице, число столбцов равно числу столбцов во второй матрице.

Свойства умножения матриц. Точно так же, как композиция отображений не является коммутативной, произведение матриц тоже не коммутативно. Но есть ассоциативность, как и у, опять же, композиции. То же самое можно проверить, приведя контр-пример, и проведя ту пые вычисления. Также есть свойство дистрибутивности: $(A + B) C = AC + BC$ и $A(B + C) = AB + AC$. Доказывается просто, если расписать произведение матриц по формуле:

\[\sum_{k = 1}^s (a_{ik} + b_{ik}) c_{kj} = \sum_{k = 1}^s a_{ik} c_{kj} + \sum_{k = 1}^s b_{ik} c_{kj}\]

---

Транспонирование матриц

Транспонирование матриц — это замена в матрице строк на столбцы, а столбцов на строки. Выглядит вот так:

\[A = \left(\begin{matrix} a_{11} & a_{12} & \dots & a_{1m} \\ a_{21} & a_{22} & \dots & a_{2m} \\ \dots & \dots &\dots &\dots \\ a_{n1} & a_{n2} & \dots & a_{nm} \end{matrix}\right),\,\, A^T = \left(\begin{matrix} a_{11} & a_{21} & \dots & a_{n1} \\ a_{12} & a_{22} & \dots & a_{n2} \\ \dots & \dots &\dots &\dots \\ a_{1m} & a_{2m} & \dots & a_{nm} \end{matrix}\right)\]

(Мне вообще проще думать об этом не как о перестановке столбцов и строк, а как об отражении матрицы относительно диагонали, продлённой за границы матрицы, если это необходимо. Эти все дурацкие столбцы и строки вообще не укладываются в голову. Ну, и так получается, что если $(b_{ij}’)$ — транспонированная матрица, то $b_{ij}’ = b_{ji}$.)

Свойства транспонирования матриц:

• Очевидно, из матрицы $n \times m$ после транспонирования получается матрица $m \times n$.

• $(A^T)^T = A$

• $(A + B)^T = A^T + B^T$

• $(\lambda A)^T = \lambda A^T$

• $(AB)^T = B^T A^T$. Проверяется просто по определению:

  \[C = AB,\,\, D = B^T A^T\\ c_{ij} = \sum_{k = 1}^n a_{ik} b_{kj},\,\, d_{ji} = \sum_{k=1}^n b'_{jk} a'_{ki} = \sum_{k = 1}^n a_{ik} b_{kj}\]

• Ну, и в целом получается, что $(A_1 A_2 \dots A_n)^T = A_n^T A_{n-1}^T \dots A_1^T$.

• $\text{rank}A^T = \text{rank}A$ (просто из того, что ранг по столбцам равен рангу по строкам).

Оглавление

• Векторные пространства строк и столбцов
  • Какие-то общие штуки

Векторные пространства строк и столбцов

---

2.1 в первой книжке кострикина

определение векторного (линейного) пространства, его аксиомы, следствия из них, линейная комбинация и линейная оболочка, свойства линейных оболочек (альтернативное определение линейной оболочки множества векторов), пересечение/объединение линейных оболочек

линейная (не)зависимость, свойства линейной независимости (линейная зависимость части системы векторов, линейная зависимость <=> один вектор можно выразить через остальные, добавление вектора к линейной не/зависимой системе векторов)

базис линейной оболочки, стандартный базис, единственность разложения вектора по базису, базис - наибольший линейно независимый набор векторов, существование базиса и размерность линейной оболочки (независимость от базиса и то, что размерность линейных оболочек в R^n не может быть больше n)

---

Какие-то общие штуки

Векторное пространство строк. Множество $\mathbb{R}^n$ называется векторным пространством длины $n$ над $\mathbb{R}$. Элементы векторного пространства называются векторами. Векторное пространство рассматривается вместе с операциями сложения векторов (просто по-элементно) и умножения на скаляры (скаляр — в данном случае элемент $\mathbb{R}$). По сути векторы являются $1 \times n$ матрицами. Вот определения операций:

\[X + Y = (x_1 + y_1, \dots, x_n + y_n) \\ \lambda X = (\lambda x_1, \dots, \lambda x_n)\]

Нулевой вектор $(0, \dots, 0)$ будет обозначаться просто как $0$.

Векторное (линейное) пространство $(\mathbb{R}, \mathbb{R}^n)$ определяется с помощью следующих аксиом:

1. $X + Y = Y + X$ — коммутативность для сложения.
2. $(X + Y) + Z = X + (Y + Z)$ — ассоциативность для сложения.
3. $\exists 0 \in \mathbb{R}^n: X + 0 = X,\, \forall X \in \mathbb{R}^n$ — существование нулевого элемента по сложению (единственность выводится).
4. $\forall X \,\, \exists (-X) \in \mathbb{R}^n : X + (-X) = 0$ — существование обратного по сложению (единственность выводится).
5. $\exists 1 \in \mathbb{R} : 1X = X, \forall X \in \mathbb{R}^n$ — существование нейтрального по умножению на скаляр (единственность выводится).
6. $(\alpha\beta)X = \alpha(\beta X)$ — ассоциативность умножения на скаляр.
7. $(\alpha + \beta)X = \alpha X + \beta X$ — дистрибутивность.
8. $\alpha(X + Y) = \alpha X + \alpha Y$ — другая дистрибутивность.

---

Линейные комбинации и линейная оболочка. Вектор $X = \alpha_1 X_1 + \dots + \alpha_k X_k$ называется линейной комбинацией векторов ${X_i}$ с коэффициентами ${\alpha_i}$. Линейной оболочкой называется множество всех линейных комбинаций заданной системы векторов $X_1, \dots, X_k$ и обозначается как $\left<X_1, \dots, X_k\right>$. Очевидно, линейная оболочка замкнута относительно операций сложения векторов и умножения на скаляр.

Под $\left<S\right>$, где $S \subset \mathbb{R}^n$, подразумевается совокупность всех линейных комбинаций конечных систем векторов из $S$ (короче, берутся все возможные конечные подмножества векторов из $S$, и берётся совокупность их линейных оболочек).

Свойства линейных оболочек:

• Если $V$ — линейная оболочка, то $\left< V \right> = V$ (следует из замкнутости линейных оболочек относительно сложения и умножения на скаляр).

• Если $V$ — какая-то линейная оболочка, то $S \subset V \implies \left<S\right> \subset V$ (тоже следует из замкнутости относительно сложения и умножения).

• Альтернативное определение линейной оболочки: $\left< S \right> = \cap_{S \subset V} V$, где $V$ — это произвольные линейные оболочки.

  Пусть $X \in \left<S\right> \subset V,\, \forall V : S \subset V$, из этого следует вложенность в одну сторону (следует из предыдущего свойства). А в обратную сторону не знаю, как доказывать, но, видимо, это очевидно? Можно доказать, что пересечение линейных оболочек является линейной оболочкой: $X,Y \in \cap V \implies \alpha X + \beta Y \in \cap V,\, \forall \alpha,\beta \in \mathbb{R}$, потому что $X,Y \in V$ для каждой линейной оболочки, содержащей $S$, и линейные оболочки замкнуты относительно основных операций, так что они остаются внутри.

  При этом объединение линейных оболочек в общем случае линейной оболочкой не является, потому что линейная комбинация элементов из разных линейных оболочек может вылезти куда угодно. Например, если взять линейные оболочки $U = {(\lambda,0) \mid \lambda \in \mathbb{R}}$ и $V = {(0, \lambda) \mid \lambda \in \mathbb{R}}$, то их объединение линейной оболочкой не будет: $(1,0) \in U,\,\, (0, 1) \in V$, но при этом $(1, 1) \not \in U \cup V$.

---

Линейная зависимость. Система векторов $X_1, \dots, X_k$ называется линейно зависимой, если найдутся $k$ одновременно не равных нулю скаляров $\alpha_1, \dots, \alpha_k$ таких, что $\alpha_1 X_1 + \dots + \alpha_k X_k = 0$. Вот это последнее равенство — это линейная зависимость векторов, и, если коэффициенты не равны нулю, то будем говорить, что эта зависимость нетривиальна.

Примеры:

• Набор единичных векторов $E_{(1)} = (1, 0, \dots, 0), E_{(2)} = (0, 1, 0, \dots, 0),\dots,E_{(n)} = (0, 0, \dots,0, 1)$ всегда линейно независим, иначе нельзя составить такую линейную комбинацию, чтобы получился нулевой вектор.
• Система из одного ненулевого вектора тоже всегда линейно независима.

Утверждения, связанные с линейной независимостью:

• Система векторов с линейно зависимой подсистемой сама будет линейно зависима.

  Ну, тут очевидно, достаточно выставить правильные коэффициенты в линейной комбинации для линейно зависимой подсистемы, а остальные можно просто обнулить.

• Любая часть линейно независимой системы векторов линейно независима.

  Если предположить обратное, то из этого будет следовать линейная зависимость всей системы.

• Система векторов является линейно зависимой тогда и только тогда, когда хотя бы один из векторов системы может быть выражен линейной комбинацией других.

  Очевидно, если система векторов линейно зависима, то есть нетривиальная нулевая линейная комбинация:

  \[\alpha_1 X_1 + \dots + \alpha_k Xk = 0,\, \alpha_j \not = 0 \\ X_j = -\frac{\alpha_1}{\alpha_j}X_1 + \dots + \widehat{X_j} + \dots -\frac{\alpha_k}{\alpha_j} X_k \\\]

  (Вот эта запись с шапочкой означает, что $j$-ый элемент пропускается. Иначе можно было бы написать левый и правый от пропускаемого элементы, но это слишком громоздкая запись.)

  Ну, и наоборот, если какой-то из векторов выражается через другие, то: либо он выражается просто как $X_k = 0 X_1 + \dots\ + \widehat{X_j} + \dots + 0X_k = 0$ — тогда система векторов будет линейно зависимой (потому что любая система, в которой есть хотя бы один нулевой вектор, будет линейно зависимой). Если же выражается нетривиально, то, ну, просто понятно всё.

• Если $X_1,\dots,X_k$ линейно независимы, а $X_1,\dots,X_k,X$ линейно зависимы (просто добавили к системе ещё какой-то вектор), то $X$ выражается через линейную комбинацию векторов $X_1,\dots,X_k$.

  Для доказательства достаточно рассмотреть нетривиальную линейную комбинацию:

  \[\alpha_1 X_1 + \dots + \alpha_k X_k + \alpha X = 0\]

  Если $\alpha \not = 0$, то достаточно просто перенести $X$ направо и разделить всё выражение на $\alpha$. Если же $\alpha = 0$, то это бы означало, что и $\alpha_1 = 0, \dots,\,\alpha_k = 0$ в силу линейной независимости $X_1, \dots, X_k$, и это всё противоречит с линейной зависимостью $X_1, \dots, X_k, X$.

• Если $X_1, \dots, X_k$ линейно независимы, и нельзя выразить $X_{k+1}$ через эти вот векторы $X_1, \dots, X_k$, то система векторов $X_1, \dots, X_{k+1}$ тоже будет линейно независимой.

  Потому что, будь они линейно зависимой системой, то по предыдущему утверждению это бы означало, что $X_{k+1}$ выражается через остальные векторы, а это противоречит условию.

---

Базис. Размерность. Пусть $V$ — линейная оболочка в $\mathbb{R}^n$, тогда система векторов $X_1, \dots, X_m$ называется базисом для $V$, если она линейно независима и её линейная оболочка совпадает с $V$ (иначе говоря, является порождающей для $V$). Базис полезен тем, что через него единственным образом через линейную комбинацию выражается любой вектор из $V$. То, что оно как-то выражается, — это очевидно (по определению), а единственность следует из линейной независимости:

\[\text{Рассмотрим два разложения вектора } X \text{ по базису:} \\ X = \alpha_1 X_1 + \dots + \alpha_m X_m, \,\, X = \beta_1 X_1 + \dots + \beta_m X_m \\ (\alpha_1 - \beta_1) X_1 + \dots + (\alpha_m - \beta_m) X_m = 0 \implies \alpha_i = \beta_i,\forall i\]

$\mathbb{R}^n$ — это, очевидно, тоже линейная оболочка единичных векторов. И эти единичные вектора также являются базисом $\mathbb{R}^n$ (порождающий плюс линейно независимый). ${E_{(1)}, E_{(2)},\dots, E_{(n)}}$ — стандартный базис, но базис может не быть единственным. Например, есть ещё вот такой базис:

\[E'_{(1)} = E_{(1)} \\ E'_{(2)} = E_{(1)} + E_{(2)} \\ E'_{(3)} = E_{(1)} + E_{(2)} + E_{(3)} \\ \dots\\ E'_{(n)} = E_{(1)} + \dots + E_{(n)}\]

(Ну, тут легко проверить то, что этот набор векторов порождающий и линейно независимый.)

---

Лемма. Пусть $V$ — линейная оболочка с базисом $X_1, \dots, X_m$. Тогда, если $Y_1, \dots, Y_k$ — линейно независимая система из векторов из $V$, то $m \geq k$. (То есть базис — наибольший линейно независимый набор.)

Доказательство. Для начала распишем векторы ${Y_i}$ как линейные комбинации базисных векторов:

\[Y_1 = \alpha_{11} X_1 + \alpha_{12} X_2 + \dots + \alpha_{1m} X_m\\ \dots\\ Y_k = \alpha_{k1} X_1 + \alpha_{k2} X_2 + \dots + \alpha_{km} X_m\]

Будем доказывать от противного: предположим, что $k \gt m$. Составим линейную комбинацию из векторов ${Y_i}$:

\[x_1 Y_1 + \dots + x_k Y_k = [\text{раскладываем игреки по базису}] \\ = x_1(\alpha_{11} X_1 + \alpha_{12} X_2 + \dots + \alpha_{1m} X_m) + \dots + x_k (\alpha_{k1} X_1 + \alpha_{k2} X_2 + \dots + \alpha_{km} X_m)\\ = (\alpha_{11}x_1 + \dots + \alpha_{k1}x_k)X_1 + \dots + (\alpha_{1m}x_1 + \dots + \alpha_{km}x_k)X_m\]

Попробуем приравнять значение этой линейной комбинации к нуль-вектору. Для этого придётся решить систему уравнений:

\[\begin{cases} \alpha_{11}x_1 + \dots + \alpha_{k1}x_k = 0\\ \dots\\ \alpha_{1m}x_1 + \dots + \alpha_{km}x_k = 0 \end{cases}\]

Так как мы приняли, что $k > m$ (то есть в данном случае у нас переменных больше, чем уравнений), то это означает, что после приведения к ступенчатому виду у нас будут свободные неизвестные, которые могут принимать произвольные значения, а, значит, будет ненулевое решение . То есть мы нашли способ нетривиально обнулить $x_1 Y_1 + \dots + x_k Y_k$, что противоречит с тем, что ${Y_i}$ — линейно независимый набор векторов по условию.

---

Теорема. Каждая ненулевая (содержащая по крайней мере один ненулевой вектор) линейная оболочка $V \subset \mathbb{R}^n$ обладает конечным базисом. При этом все базисы оболочки $V$ состоят из одинакового числа $m \leq n$ векторов (короче, количество элементов в базисе не больше размерности R^n штуки, в которой находится линейная оболочка), и это число обозначается как $\dim V := m$ и называется размерностью линейной оболочки.

Доказательство. По условию в $V$ есть хотя бы один ненулевой вектор, обозначим его за $X_1$. Предположим, что мы нашли линейно независимую систему векторов $X_1, \dots, X_k$ (по крайней мере можно взять один единственный $X_1$, он будет линейно независим сам по себе). Если линейная оболочка выбранного набора линейно независимых векторов $\left<X_1,\dots,X_k\right>$ не совпадает с $V$, то берём $X_{k+1} : X_{k + 1} \in V,\, X_{k+1} \not \in \left< X_1, \dots, X_k \right>$. И по теореме выше набор $X_1, \dots, X_{k+1}$ тоже будет линейно независимой (добавляем к линейно независимому набору вектор, который не выражается через эти векторы).

По предыдущей лемме любой линейно независимый набор в $V$ содержит не более, чем $n$ векторов (рассматриваем линейную оболочку $\mathbb{R}^n$, в которой у нас есть стандартный базис с $n$ элементами). Так что мы не сможем бесконечно добавлять новые векторы в систему, а это означает, что, рано или поздно, она станет максимальной/порождающей. Так доказали существование базиса для линейной оболочки.

Предположим, что $Y_1, \dots, Y_s$ — ещё один базис в $V$. Тогда $s \leq m$ по предыдущей лемме, так как базис — это линейно независимая штука. И наоборот, если подставить в лемму ${X_i}$ вместо ${Y_i}$, то, получится, что $m \leq s$. Из этого следует, что $m = s$, а, значит, мы можем корректно определить размерность линейной оболочки.

Ранг системы векторов в $\mathbb{R}^n$: ${X_1, X_2,\dots}$ определяется как размерность линейной оболочки, построенной на них:

\[\text{rank} \{X_1, X_2,\dots \} := \dim\left<X_1, X_2, \dots\right>\]

Размерность линейной оболочки, состоящей только из нуль-вектора принять считать равной нулю: $\dim V := 0,\,V = {0}$.